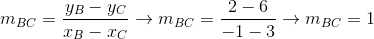Reta suporte
2 participantes
Página 1 de 1
Reta suporte
por anabperc Ter 13 Fev 2018, 15:27
A equação da reta suporte da altura relativa ao lado BC do triângulo ABC de vértices;
A(1,1), B(-1,2) e C(3,6) é:
a)x+y=0
b)x+y-2=0
c)x-y+2=0
d)x+y+2=0
e)x-y-2=0
(Se tiver como explicar por passo a passo agradeço!)
A(1,1), B(-1,2) e C(3,6) é:
a)x+y=0
b)x+y-2=0
c)x-y+2=0
d)x+y+2=0
e)x-y-2=0
(Se tiver como explicar por passo a passo agradeço!)
anabperc- Iniciante
- Mensagens : 47
Data de inscrição : 08/06/2016
Idade : 24
Localização : Brasil
Re: Reta suporte
por Giovana Martins Ter 13 Fev 2018, 16:02
Seja a reta BC, a qual passa pelos pontos B(-1,2) e C(3,6).
Cálculo do coeficiente angular da reta BC:
A reta que contém a altura relativa ao lado BC é perpendicular à reta que contém o lado BC, logo, o coeficiente angular da reta que contém a altura relativa ao lado BC é dado por:
Sabendo que a reta que contém a altura que queremos encontrar passa pelo ponto A(1,1) e, tendo o seu coeficiente angular, podemos encontrar a sua equação de reta como é mostrado a seguir:
Em um plano cartesiano fica assim:
Ana, se algo não tiver ficado claro é só falar.
Giovana Martins- Grande Mestre
- Mensagens : 7645
Data de inscrição : 15/05/2015
Idade : 23
Localização : São Paulo
Re: Reta suporte
por anabperc Ter 13 Fev 2018, 16:55
Obrigada, entendi mt bem!!!Giovana Martins escreveu:Seja a reta BC, a qual passa pelos pontos B(-1,2) e C(3,6).Cálculo do coeficiente angular da reta BC:A reta que contém a altura relativa ao lado BC é perpendicular à reta que contém o lado BC, logo, o coeficiente angular da reta que contém a altura relativa ao lado BC é dado por:Sabendo que a reta que contém a altura que queremos encontrar passa pelo ponto A(1,1) e, tendo o seu coeficiente angular, podemos encontrar a sua equação de reta como é mostrado a seguir:Em um plano cartesiano fica assim:Ana, se algo não tiver ficado claro é só falar.
anabperc- Iniciante
- Mensagens : 47
Data de inscrição : 08/06/2016
Idade : 24
Localização : Brasil
Giovana Martins- Grande Mestre
- Mensagens : 7645
Data de inscrição : 15/05/2015
Idade : 23
Localização : São Paulo
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
