Esfera e cilindro

Determine a razão entre os volumes de uma esfera e do cilindro equilátero nela inscrito.

Gabarito: (4√2)/3

Bom dia!


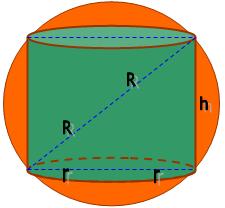
Essa imagem ajuda bastante no entendimento da questão, já que forma um triangulo retângulo podemos aplicar Pitágoras:
(2r)² + h² = (2R)²
Perceba que a questão diz que o cilindro é equilátero, portanto a altura é igual ao diâmetro que por sua vez é duas vezes o raio, então temos:
(2r)² + (2r)² = (2R)²
8r² = 4R²
2r² = R²
r√2 = R

Utilizando a fórmula de volume para a esfera e substituindo R por r√2:
Vs = 4piR³ /3
Vs = 4pi(r√2)³ /3
Vs = 8pi*r³√2 /3

E a do cilindro, sendo h = 2r:
Vc = pi*r²h
Vc = pi*r²*2r
Vc = 2pi*r³

Para achar a razão basta dividir o volume da esfera pelo volume do cilindro:
Razão = Vs/Vc
Razão = (8pi*r³√2 /3) / 2pi*r³
Razão = (4√2)/3


Espero ter ajudado, abraços!