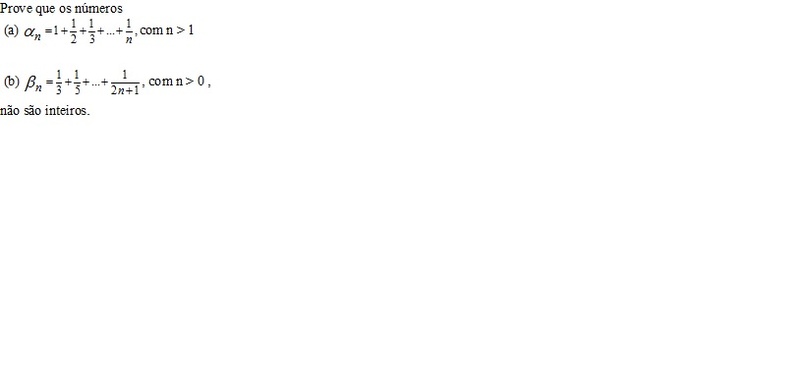divisibilidade - 2
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 divisibilidade - 2
divisibilidade - 2
Prove que os números an e bn não são inteiros
(a) an = 1 + 1/2 +1/3 + ... + 1/n, com n > 1
(b) bn = 1/3 + 1/5 + ...+ 1/(2n + 1), com n > 0
(a) an = 1 + 1/2 +1/3 + ... + 1/n, com n > 1
(b) bn = 1/3 + 1/5 + ...+ 1/(2n + 1), com n > 0
Cristina Lins- Jedi

- Mensagens : 470
Data de inscrição : 01/03/2012
Idade : 66
Localização : Itapetininga - SP
 Re: divisibilidade - 2
Re: divisibilidade - 2
@Edit.
Eu li "Prove que os números an e bn são inteiros
Eu li "Prove que os números an e bn são inteiros

superaks- Mestre Jedi

- Mensagens : 525
Data de inscrição : 27/06/2016
Idade : 23
Localização : São Paulo, Guarulhos, Brasil
Cristina Lins- Jedi

- Mensagens : 470
Data de inscrição : 01/03/2012
Idade : 66
Localização : Itapetininga - SP
 Re: divisibilidade - 2
Re: divisibilidade - 2
(a)
Considere mmc(1, 2, 3, ..., n) = 2^k . m com m ímpar para n > 1 e k ≥ 1.
Suponha agora que 1 + 1/2 + ... + 1/n seja inteiro para para algum n > 1.
Somando todas as frações, temos:
t = 2^k . m/1 + [(2^k . m)/2]/(2^k . m) + ... + [(2^k . m)/n]/(n)
Onde t é inteiro.
Eu afirmo que o numerador de somente uma dessas parcelas tem que ser impar. Porque ?
Vai existir uma parcela cujo o numerador é divisível por 2^k (lembrando que 2^k é a maior potência que aparece no MMC), vamos chamar esse numerador de j. O próximo menor numerador que 2^k divide, seria 2j, mas ele não pode estar nessa parcela, pois se 2^k divide j, então 2^(k + 1) divide 2j, só que 2^k já é a maior potência de 2 que aparece no numerador.
Então eu vou ter n - 1 parcas par e 1 número ímpar no numerador, logo, a soma dessas parcelas no numerador tem que ser um número ímpar, digamos 2p - 1.
t = (2p - 1)/(2^k . m)
2^k não pode dividir 2p - 1, pois 2p - 1 é ímpar, logo, t não pode ser inteiro, portanto absurdo !.
Então an não pode ser inteiro para n > 1.
(b)
Seja mmc(3, 5, ..., 2n + 1) = 3^k . m, onde mdc(m, 3^k) = 1 para n > 0 e k ≥ 1.
Suponha que exista um n tal que aquela soma seja inteira.
Logo:
t = 1/3 + 1/5 + .. + 1/(2n + 1) = [(3^k . m/3)]/(3^k . m) + [(3^k . m)/5]/(3^k . m) + ... + [(3^k . m)/(2n + 1)]/(3^k . m)
Afirmo que existe somente uma fração cujo o numerador é divisível por 3^k (a maior potência de 3 que aparece no MMC). Chame esse número que é divisível por 3^k de j. 2j também é divisível por 3^k, porém, 2j não pode participar dessa soma, pois 2j é par e não existe número par nessas parcelas. Então o próximo seria 3j, mas aí teríamos que 3^(k + 1) dividiria 3j, logo, 3j não faz parte dessa parcela.
Então eu teria que 3 dividiria, n - 1 parcelas mas não 1. Então aquela soma ficaria:
t = y/(3^k . m)
Onde y não é divisível por 3, mas 3^k é pelo menos 3, portanto, absurdo !
Logo, bn não pode ser inteiro para nenhum n.
Se ficou com dúvida em alguma parte, marque o trecho e mande
Considere mmc(1, 2, 3, ..., n) = 2^k . m com m ímpar para n > 1 e k ≥ 1.
Suponha agora que 1 + 1/2 + ... + 1/n seja inteiro para para algum n > 1.
Somando todas as frações, temos:
t = 2^k . m/1 + [(2^k . m)/2]/(2^k . m) + ... + [(2^k . m)/n]/(n)
Onde t é inteiro.
Eu afirmo que o numerador de somente uma dessas parcelas tem que ser impar. Porque ?
Vai existir uma parcela cujo o numerador é divisível por 2^k (lembrando que 2^k é a maior potência que aparece no MMC), vamos chamar esse numerador de j. O próximo menor numerador que 2^k divide, seria 2j, mas ele não pode estar nessa parcela, pois se 2^k divide j, então 2^(k + 1) divide 2j, só que 2^k já é a maior potência de 2 que aparece no numerador.
Então eu vou ter n - 1 parcas par e 1 número ímpar no numerador, logo, a soma dessas parcelas no numerador tem que ser um número ímpar, digamos 2p - 1.
t = (2p - 1)/(2^k . m)
2^k não pode dividir 2p - 1, pois 2p - 1 é ímpar, logo, t não pode ser inteiro, portanto absurdo !.
Então an não pode ser inteiro para n > 1.
(b)
Seja mmc(3, 5, ..., 2n + 1) = 3^k . m, onde mdc(m, 3^k) = 1 para n > 0 e k ≥ 1.
Suponha que exista um n tal que aquela soma seja inteira.
Logo:
t = 1/3 + 1/5 + .. + 1/(2n + 1) = [(3^k . m/3)]/(3^k . m) + [(3^k . m)/5]/(3^k . m) + ... + [(3^k . m)/(2n + 1)]/(3^k . m)
Afirmo que existe somente uma fração cujo o numerador é divisível por 3^k (a maior potência de 3 que aparece no MMC). Chame esse número que é divisível por 3^k de j. 2j também é divisível por 3^k, porém, 2j não pode participar dessa soma, pois 2j é par e não existe número par nessas parcelas. Então o próximo seria 3j, mas aí teríamos que 3^(k + 1) dividiria 3j, logo, 3j não faz parte dessa parcela.
Então eu teria que 3 dividiria, n - 1 parcelas mas não 1. Então aquela soma ficaria:
t = y/(3^k . m)
Onde y não é divisível por 3, mas 3^k é pelo menos 3, portanto, absurdo !
Logo, bn não pode ser inteiro para nenhum n.
Se ficou com dúvida em alguma parte, marque o trecho e mande

superaks- Mestre Jedi

- Mensagens : 525
Data de inscrição : 27/06/2016
Idade : 23
Localização : São Paulo, Guarulhos, Brasil
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos