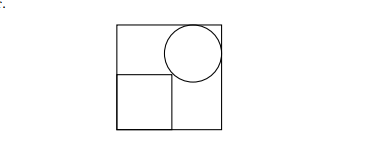
Raio do Círculo

por **Kayo Emanuel Salvino** Dom 19 Nov 2017, 12:47

Na figura abaixo temos dois quadrados, um de lado dois e outro de lado um. Determine o raio do cíırculo que é tangente aos lados do maior e passa pelo vértice do menor

Agradeço desde já.

por **Elcioschin** Dom 19 Nov 2017, 13:49

Seja ABCD o quadrado com A sendo o vértice superior esquerdo e D o inferior esquerdo
Seja E, F os vértices do quadrado menor sobre AD e CD e P o vértice sobre a circunferência de centro O
Sejam M, N os pontos de tangência da circunferência com AB e BC

Trace DPOB, OM e ON

DE = EP = PF = FD = 1 ---> DP = √2
AB = BC = CD = DA = 2 ---> DB = 2.√2
OM = ON = OP = BM = BN = r ---> OB = r.√2

DP + OP + OB = DB ---> √2 + r + r.√2 = 2.√2 ---> r.(√2 + 1) = √2 ---> r = √2/(√2 + 1) --->

r = √2.(√2 - 1)/(√2 + 1).(√2 - 1) ---> r = 2 - √2

por **Kayo Emanuel Salvino** Dom 19 Nov 2017, 18:19

Grato pelas explicações!!

por SpaceFunction Dom 19 Nov 2017, 21:57

Também há como resolver por geometria analítica.

Primeiro, para uma compreensão facilitada, rotacione a imagem em 180º. Em seguida, gere eixos cartesianos arbitrários nos lados tangentes à circunferência.

Como o círculo tangencia os eixos, é evidente que Xo = Yo = R. Portanto, sua equação é reduzida a:

λ: (x-R)² + (y-R)² = R²

Finalmente, um dos vértices do quadrado menor faz parte da circunferência. Chamando-o de P, nota-se que suas coordenadas cartesianas são P(1,1).

(1-R)² + (1-R²) = R²
2(1-R)² = R²
(1-R)√2 = R
√2 - R√2 = R
R = √2/(√2+1)

R = 2-√2