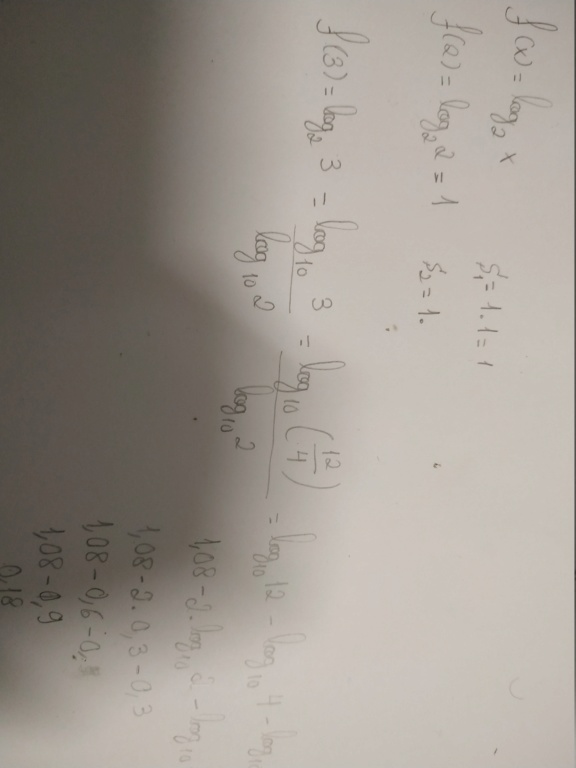Função Logarítmica
4 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Função Logarítmica
Função Logarítmica

A curva da figura representa o gráfico da função f(x) =log2x. Dados: log102 ≅ 0,30 e log10 12 ≅ 1,08. Com base nesses dados, a soma das áreas dos dois retângulos hachurados é, aproximadamente:
geometry- Iniciante
- Mensagens : 48
Data de inscrição : 18/05/2017
Idade : 24
Localização : São Paulo, Paulínia, Brasil
 Re: Função Logarítmica
Re: Função Logarítmica
Ok!
Temos que ver algumas coisitas antes de mais nada, e o que seria Ronaldo?
Repara que a area do rectangulo e dado por c*l, entao temos que a base do primeiro rectangularzinho e dado por 3-2=1, pois a distante esta ENTRE dois pontos(atencao a isso cara), e temos que do outro rectangulo ja maior, a base e dada por 4-3=1, pela mesma razao acima. Legal ate aqui? Ok !
Repara um detalhe muito importante, que essa altura esta batendo nos pontos x=3 e x=2, no pequeno rectangulo( se vc olhar a altura do lado direito e esquerdo), e como trata-se de uma funcao do tipo y= logx na base, 2, podemos exprimir essa altura nesses pontos em funcao dessa propria funcao, ou seja fazendo como haviamos feito antes( oque Ronaldo) aquela diferenca entre os pontos, ou seja log de 4 na base 2 - log de 3 na base 2 ficando com 0,41 aproximadamente.
Conclusao final: A area 1= (3-2) *( log de 3 na base 2 - log de 2 na base 2)
e a area 2= (4-3)*( log de 4 na base 2 - log de 3 na base 2), logo a soma das areas sera dada por Total= A1 + A2.
Obs especial: o Enunciado esta dando dados de um logaritmo decimal, entao eu acho que esse grafico na verdade e o grafico de y=logx, e nao de logaritmo de x na base 2.
Temos que ver algumas coisitas antes de mais nada, e o que seria Ronaldo?
Repara que a area do rectangulo e dado por c*l, entao temos que a base do primeiro rectangularzinho e dado por 3-2=1, pois a distante esta ENTRE dois pontos(atencao a isso cara), e temos que do outro rectangulo ja maior, a base e dada por 4-3=1, pela mesma razao acima. Legal ate aqui? Ok !
Repara um detalhe muito importante, que essa altura esta batendo nos pontos x=3 e x=2, no pequeno rectangulo( se vc olhar a altura do lado direito e esquerdo), e como trata-se de uma funcao do tipo y= logx na base, 2, podemos exprimir essa altura nesses pontos em funcao dessa propria funcao, ou seja fazendo como haviamos feito antes( oque Ronaldo) aquela diferenca entre os pontos, ou seja log de 4 na base 2 - log de 3 na base 2 ficando com 0,41 aproximadamente.
Conclusao final: A area 1= (3-2) *( log de 3 na base 2 - log de 2 na base 2)
e a area 2= (4-3)*( log de 4 na base 2 - log de 3 na base 2), logo a soma das areas sera dada por Total= A1 + A2.
Obs especial: o Enunciado esta dando dados de um logaritmo decimal, entao eu acho que esse grafico na verdade e o grafico de y=logx, e nao de logaritmo de x na base 2.
Última edição por Ronaldo Miguel em Qui 21 Set 2017, 16:47, editado 1 vez(es)
Ronaldo Miguel- Mestre Jedi

- Mensagens : 570
Data de inscrição : 27/03/2016
Idade : 26
Localização : Moçambique-Cidade de Maputo
 Re: Função Logarítmica
Re: Função Logarítmica
f(1) = log21 --> f(1) = 0
f(2) = log22 --> f(2) = 1
f(3) = log23
f(4) = log24 --> f(4) = 2
log1012 = log10(3.2²) ---> 1,08 = log103 + 2.log102 ---> 1,08 = log103 + 0,60 ---> log103 = 0,48
log23 = log103/log102 ---> log23 = 0,48/0,30 ---> log23 = 1,6
S(2, 3) = (3 - 2).f(2) = 1.1 = 1
S(3, 4) = (4 - 3).f(3) = 1.1,6 - 1,6
S = 1 + 1,6 ---> S = 2,6
f(2) = log22 --> f(2) = 1
f(3) = log23
f(4) = log24 --> f(4) = 2
log1012 = log10(3.2²) ---> 1,08 = log103 + 2.log102 ---> 1,08 = log103 + 0,60 ---> log103 = 0,48
log23 = log103/log102 ---> log23 = 0,48/0,30 ---> log23 = 1,6
S(2, 3) = (3 - 2).f(2) = 1.1 = 1
S(3, 4) = (4 - 3).f(3) = 1.1,6 - 1,6
S = 1 + 1,6 ---> S = 2,6

Elcioschin- Grande Mestre

- Mensagens : 73163
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
mariana yasmin gosta desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» Função logaritmica e função exponencial (teórica).
» Função Logarítmica
» Função logarítmica
» Função logarítmica
» Função Logarítmica
» Função Logarítmica
» Função logarítmica
» Função logarítmica
» Função Logarítmica
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos