Geometria Espacial

por LuizLMA Sex 28 Jul 2017, 21:03

Um retângulo tem 10 m de perímetro e 6 m² de área. O sólido gerado com a rotação em turbo do seu menor lado terá, em m², uma área total de
A)10π
B)15π
C)20π
D)30π
E)12π

por **Victor011** Sex 28 Jul 2017, 23:47

Vamos primeiro descobrir os lados a e b do retângulo. Veja:

\\\begin{cases}2a+2b=10\;\to\;b=5-a\;\;(1)\\a.b=6\;\;(2)\end{cases}\\\\\text{Substituindo }(1)\text{ em }(2):\\\\a.(5-a)=6\\\\a^2-5a+6=0 \;\to\;a=2\;e\;b=3

Agora vamos rotacionar o retângulo em torno do menor lado:

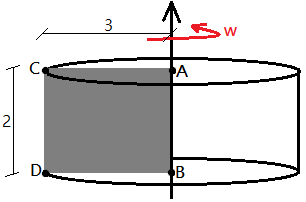
Note que o sólido formado é um cilindro com raio da base 3 e altura 2. A área lateral do cilindro pode ser calculada como a soma das áreas das faces esféricas de cima e de baixo mais um "retângulo" dobrado em volta do cilindro preso pelas pontas em CD. note que esse retângulo possui como um dos lados a própria altura CD=2 e o outro lado é o comprimento da circunferência, que vale 2πR=6π. Logo, a área lateral do cilindro será:

\\S=\pi.R^2+\pi.R^2+h.2\pi.R\\\\S=2.\pi.3^2+2.6.\pi\\\\\boxed{S=30\pi}

Geometria Espacial

Geometria Espacial

Re: Geometria Espacial

Um fórum livre e democrático.