Questão de radiciação

por Shelly ws Qua 05 Jul 2017, 21:17

Simplificando a expressão $Questão de radiciação Gif$ obtém-se:

a)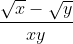 $Questão de radiciação Gif$

b)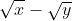 $Questão de radic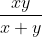iação Gif$

c) $Questão d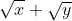e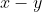 radiciação Gif$

d) $Questão de radiciação Gif$

e) $Questão de radiciação Gif$

Obs: x>0 , y>0 e x≠y
Resposta: D

Eu fiz a questão mas pra mim deu B, então vi umas resoluções da questão mas não entendi muito bem, então expliquem passo a passo por favor?
Obrigada desde já.

por **Elcioschin** Qua 05 Jul 2017, 21:31

Numerador:

N = √(x/y) - √(y/x) = √x/√y - √y/√x = (√x.√x - √y.√y)/√(x.y) = (x - y)/√(x.y)

Denominador:

D = √(1/y) - √(1/x) = 1/√y - 1/√x = (√x - √y)/√(x.y)

N/D = (x - y)/(√x - √y)

Para você entender melhor vou fazer √x = a ---> x = a² e √y = b ---> y = b²

N/D = (a² - b²)/(a - b) = (a + b).(a - b)/(a - b) --->

N/D = a + b ---> N/D = √x + √y ---> Alternativa D

Fazendo direto, sem a as substituições:

N/D = (x - y)/(√x - √y) ---> N/D = (√x + √y).(√x - √y)/(√x - √y) --->

N/D = √x + √y

Questão de radiciação

Questão de radiciação

Re: Questão de radiciação

Um fórum livre e democrático.