IFSP 2011 - Encontrar a Equação da Reta
3 participantes
Página 1 de 1
 IFSP 2011 - Encontrar a Equação da Reta
IFSP 2011 - Encontrar a Equação da Reta
Considere duas retas, r e s, passando pelo ponto (3;1) e equidistantes da origem do plano cartesiano. Se a equação da reta r é y = 1, então qual é a equação da reta s ?
Não entendi o que é "equidistantes da origem do plano cartesiano"
Não entendi o que é "equidistantes da origem do plano cartesiano"
- Resposta:
- 3x-4y-5=0
AlexSaraiva- Iniciante
- Mensagens : 27
Data de inscrição : 28/02/2016
Idade : 35
Localização : São Paulo
 Re: IFSP 2011 - Encontrar a Equação da Reta
Re: IFSP 2011 - Encontrar a Equação da Reta

____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: IFSP 2011 - Encontrar a Equação da Reta
Re: IFSP 2011 - Encontrar a Equação da Reta
Oi Alex, tudo bem?
As retas são equidistantes da origem do plano significa que as distâncias da origem O(0,0) até as retas, devem ser as mesmas.
Lembrando que sempre que um problema fala ''distância'' ele está se referindo ao comprimento do segmento de reta que é perpendicular a determinada superfície/reta.
Observe a figura :

Como a distância da reta r à origem é 1, então a distância da reta s à origem também deve ser 1. Assim, AO = 1.
Além disso, o B é o ponto em que s corta o eixo x e portanto B( x1 ; 0).
A equação da reta s pode ser escrita da forma:
y = ax + b e substituindo o ponto B na equação chegamos em: 0 = ax1 + b → x1 = -b / a
Assim o segmento OB tem medida -b / a
A medida do segmento BD é tal que BD = OD - OB
BD = 3 - OB
BD = 3 + (b/a)
Veja que os triângulos OAB e CDB são congruentes pelo caso ALA. Assim o comprimento de AB é igual ao comprimento de BD.
Então BA = 3 + (b/a)
Aplicando o teorema de pitágoras no triângulo OBA, vem que:
^{2}=1^{2}+\bigg(3+\frac{b}{a}\bigg)^{2}\\\\\rightarrow&space;\cancel{\frac{b^{2}}{a^{2}}}=1+9+\frac{6b}{a}+\cancel{\frac{b^{2}}{a^{2}}}\\\\\rightarrow&space;6b=-10a\\\\\rightarrow&space;\boxed{b=-\frac{5}{3}a}\:&space;\:&space;\:&space;\:&space;\:&space;\:&space;\:&space;\:&space;(1))
Substituindo o ponto (3,1) na equação da reta s:
1 = 3a + b (2)
De (1) em (2), temos:
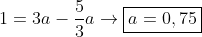
Subsituindo de volta em (2):
1 = 2,25 + b → b = -1,25
Então a equação de s é: y = 0,75x - 1,25
Ou 3x - 4y - 5 = 0
Um abraço
As retas são equidistantes da origem do plano significa que as distâncias da origem O(0,0) até as retas, devem ser as mesmas.
Lembrando que sempre que um problema fala ''distância'' ele está se referindo ao comprimento do segmento de reta que é perpendicular a determinada superfície/reta.
Observe a figura :

Como a distância da reta r à origem é 1, então a distância da reta s à origem também deve ser 1. Assim, AO = 1.
Além disso, o B é o ponto em que s corta o eixo x e portanto B( x1 ; 0).
A equação da reta s pode ser escrita da forma:
y = ax + b e substituindo o ponto B na equação chegamos em: 0 = ax1 + b → x1 = -b / a
Assim o segmento OB tem medida -b / a
A medida do segmento BD é tal que BD = OD - OB
BD = 3 - OB
BD = 3 + (b/a)
Veja que os triângulos OAB e CDB são congruentes pelo caso ALA. Assim o comprimento de AB é igual ao comprimento de BD.
Então BA = 3 + (b/a)
Aplicando o teorema de pitágoras no triângulo OBA, vem que:
Substituindo o ponto (3,1) na equação da reta s:
1 = 3a + b (2)
De (1) em (2), temos:
Subsituindo de volta em (2):
1 = 2,25 + b → b = -1,25
Então a equação de s é: y = 0,75x - 1,25
Ou 3x - 4y - 5 = 0
Um abraço
igorrudolf- Jedi

- Mensagens : 434
Data de inscrição : 10/09/2014
Idade : 28
Localização : São Paulo - São Paulo
 Re: IFSP 2011 - Encontrar a Equação da Reta
Re: IFSP 2011 - Encontrar a Equação da Reta
Valeu
Muito Obrigado

Muito Obrigado
AlexSaraiva- Iniciante
- Mensagens : 27
Data de inscrição : 28/02/2016
Idade : 35
Localização : São Paulo
 Tópicos semelhantes
Tópicos semelhantes» Equação da reta normal à reta tangente
» ( ENEM 2011 ) distância entre pontos e reta
» Ponto e reta (equação da reta)
» Questão - Equação da reta e equação da circunferência
» (CN - 2011) Equação
» ( ENEM 2011 ) distância entre pontos e reta
» Ponto e reta (equação da reta)
» Questão - Equação da reta e equação da circunferência
» (CN - 2011) Equação
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












