AFA 2003 FUNÇÃO 2° GRAU

por Kowalski Sex 12 maio 2017, 16:06

o conjunto {x pertencente R / f(x)<0} , onde f: R --> R é definida por f(x)= ax²+ 2a²x + a³

Gabarito letra B

então fica assim a < 0 de acordo com enunciado a E R negativos não nulos .
x E R / F(X) <0 quer dizer que a função é totalmente negativa ou só tem alguns pontos negativo ??

então como ficaria isso , ax² + 2a²x + a² < 0 --> a(x² +2ax + 1) < 0
a < 0
x² + 2ax + 1 < 0
Delta < 0
4a² -4 < 0
a² < 1
a < +-1 consegui fazer não

por **Elcioschin** Sex 12 maio 2017, 16:20

∆ = (2.a²)² - 2.a.a³ ---> ∆ = 0

xV = - (2.a²)/2.a ---> xV = a ---> A função tangencia o eixo x em x = a

A função é negativa ---> a < 0, com exceção do ponto (-a, 0)

O conjunto é -∞ < x < -a e - a < x < +∞

por **CaiqueF** Sex 12 maio 2017, 16:26

ax²+2a²x+a³ < 0
a(x²+2ax+a²) < 0
como a<0, entao temos que x²+2ax+a² > 0
x²+2ax+a² > 0
(x+a)² > 0
x ≠ -a

Logo, x pode assumir qualquer valor, menos -a

por Kowalski Sex 12 maio 2017, 17:36

Eu entendi a resolução do elcioschin , a do caique fiquei com dúvida nessa parte : como a<0, então temos que x²+2ax+a² > 0

I -> f(x) < 0 , significa que f(x) é negativa (-)
ax²+2a²x+a³ < 0 <<-I

ai fatorando a I fica
a(x²+2ax+a²) < 0 , para a função I ser <0 ou seja negativa

devemos ter na fatoração algo negativo multiplicando positivo

então por isso a<0 (-) e x² +2ax + a² > 0 (+) ???

por **CaiqueF** Sex 12 maio 2017, 17:39

Kowalski escreveu:Eu entendi a resolução do elcioschin , a do caique fiquei com dúvida nessa parte : como a<0, então temos que x²+2ax+a² > 0

I -> f(x) < 0 , significa que f(x) é negativa (-)
ax²+2a²x+a³ < 0 <<-I

ai fatorando a I fica
a(x²+2ax+a²) < 0 , para a função I ser <0 ou seja negativa

devemos ter na fatoração algo negativo multiplicando positivo

então por isso a<0 (-) e x² +2ax + a² > 0 (+) ???

Exatamente, se a*f(x) < 0 e sabemos que a é negativo, então pro produto ser negativo, f(x) deve, obrigatoriamente, ser maior que 0

por Kowalski Sex 12 maio 2017, 18:36

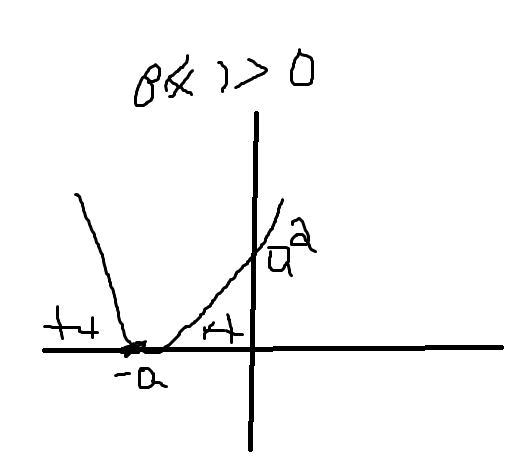
Esse é o gráfico da função x²+2ax+a² ??

então o que a questão queria era só analisar essa função e esquecer desta ax²+2a²x+a³ ?

x²+2ax+a² sabemos que é maior que zero e isso significa que a imagem dela é positiva então analisando o gráfico dela vemos que todos valores menos o -a fazem com que a imagem dê positiva e o -a não vale pois existe uma restrição a imagem tem que ser maior que zero e no caso de -a daria imagem zero . É mais ou menos isso?