Se os pontos O=(0,0), A=(6,0) e B(3,3V3) são

Se os pontos O=(0,0), A=(6,0) e B(3,3V3) são vertices de um triangulo, entao uma equação da reta que contem a bissetriz do angulo OAB é:

Não tem gabarito, ent se puderem me explicar passo-a-passo como resolver, fico grato.

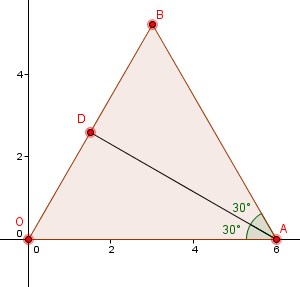
Calculando as distâncias BO, AB e AO descobrimos que o triângulo OAB é equilátero. Em um triângulo equilátero, a bissetriz de um ângulo é também uma mediana. Sejam AD a bissetriz do ângulo OAB e D o ponto médio do lado BO.

m_AD=tg 30° -> m_AD=√3/3 

Note que a reta que contém a bissetriz é decrescente, assim, o coeficiente angular dessa reta é m_AD=-√3/3.

A bissetriz AD passa pelo ponto A(6,0), logo:

y-0=m_AD(x-6) -> y=(-√3/3).(x-6) -> y=[(-x√3)/3]+2√3

Creio que este exercício também possa ser resolvido utilizando a equação das bissetrizes dos ângulos (veja o link), mas será um pouquinho mais trabalhoso.

Seja bem vindo(a) ao fórum!