Somatório e fatorial
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Somatório e fatorial
Somatório e fatorial
Prove que:
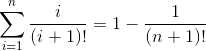
Não consigo desenvolver, além de resolver, poderiam me dar alguma dica para resolver problemas que envolvam somatório, alguma forma de pensar, não sei.
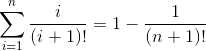
Não consigo desenvolver, além de resolver, poderiam me dar alguma dica para resolver problemas que envolvam somatório, alguma forma de pensar, não sei.

isac_pc- Recebeu o sabre de luz

- Mensagens : 102
Data de inscrição : 15/05/2016
Idade : 25
Localização : Juazeiro do Norte, CE Brasil
 Re: Somatório e fatorial
Re: Somatório e fatorial
Expandindo esse somatório de trás pra frente teriamos:
Provando por PIF.
Hipótese: 1/2! + 2/3! + 3/4! + ... + i/(i + 1)! = 1 - 1/(n + 1)!
Base = 1
1/2! = 1/2 <-------------> 1 - 1/(1 + 1)! <-> 1 - 1/2 <-> 2/2 - 1/2 <-> 1/2
Base OK!
Sabendo que funciona para um certo valor, nos convém querer saber se funcionará para um determinado valor de i, onde chamaremos de k.
Com isso queremos provar que funcionará para o sucessor de k.
1/2! + 2/3! + 3/4! + ... + k/(k + 1)! + (k + 1)/(k + 2)! = 1 - 1/[(k + 1) + 1)]!
[1/2! + 2/3! + 3/4! + ... + k/(k + 1)!] = 1 - 1/(k + 1)!
1 - 1/(k + 1)! + (k + 1)/(k + 2)! = 1 - 1/(k + 2)!
1 - (k + 2)!/(k + 1)!(k + 2)! + (k + 1)(k + 1)!/(k + 2)!(k + 1)! = 1 - 1/(k + 2)!
1 + [-(k + 2)! + (k + 1)(k + 1)!]/(k + 1)!(k + 2)! = 1 - 1/(k + 2)!
1 + [-(k + 2)(k + 1)! + (k + 1)(k + 1)!]/(k + 1)!(k + 2)! = 1 - 1/(k + 2)!
1 + {(k + 1)![-(k + 2) + (k + 1)]}/(k + 1)!(k + 2)! = 1 - 1/(k + 2)!
1 + [- k - 2 + k + 1]/(k + 2)! = 1 - 1/(k + 2)!
1 + [- 1]/(k + 2)! = 1 - 1/(k + 2)!
1 - 1/(k + 2)! = 1 - 1/(k + 2)!
Portanto a igualdade é verdadeira.
Obsv. Sei que tem uma forma de resolver isso usando soma telescópica, mas como não entendo muito sobre o assunto, vou responder usando PIF.
Provando por PIF.
Hipótese: 1/2! + 2/3! + 3/4! + ... + i/(i + 1)! = 1 - 1/(n + 1)!
Base = 1
1/2! = 1/2 <-------------> 1 - 1/(1 + 1)! <-> 1 - 1/2 <-> 2/2 - 1/2 <-> 1/2
Base OK!
Sabendo que funciona para um certo valor, nos convém querer saber se funcionará para um determinado valor de i, onde chamaremos de k.
Com isso queremos provar que funcionará para o sucessor de k.
1/2! + 2/3! + 3/4! + ... + k/(k + 1)! + (k + 1)/(k + 2)! = 1 - 1/[(k + 1) + 1)]!
[1/2! + 2/3! + 3/4! + ... + k/(k + 1)!] = 1 - 1/(k + 1)!
1 - 1/(k + 1)! + (k + 1)/(k + 2)! = 1 - 1/(k + 2)!
1 - (k + 2)!/(k + 1)!(k + 2)! + (k + 1)(k + 1)!/(k + 2)!(k + 1)! = 1 - 1/(k + 2)!
1 + [-(k + 2)! + (k + 1)(k + 1)!]/(k + 1)!(k + 2)! = 1 - 1/(k + 2)!
1 + [-(k + 2)(k + 1)! + (k + 1)(k + 1)!]/(k + 1)!(k + 2)! = 1 - 1/(k + 2)!
1 + {(k + 1)![-(k + 2) + (k + 1)]}/(k + 1)!(k + 2)! = 1 - 1/(k + 2)!
1 + [- k - 2 + k + 1]/(k + 2)! = 1 - 1/(k + 2)!
1 + [- 1]/(k + 2)! = 1 - 1/(k + 2)!
1 - 1/(k + 2)! = 1 - 1/(k + 2)!
Portanto a igualdade é verdadeira.
Obsv. Sei que tem uma forma de resolver isso usando soma telescópica, mas como não entendo muito sobre o assunto, vou responder usando PIF.

superaks- Mestre Jedi

- Mensagens : 525
Data de inscrição : 27/06/2016
Idade : 23
Localização : São Paulo, Guarulhos, Brasil
fantecele- Fera

- Mensagens : 1225
Data de inscrição : 14/09/2014
Idade : 27
Localização : Nova Venécia-ES, Brasil
 Re: Somatório e fatorial
Re: Somatório e fatorial
vlw gente!

isac_pc- Recebeu o sabre de luz

- Mensagens : 102
Data de inscrição : 15/05/2016
Idade : 25
Localização : Juazeiro do Norte, CE Brasil
 Tópicos semelhantes
Tópicos semelhantes» Somatório e fatorial
» Somatório Fatorial!
» Somatório fatorial
» Somatório
» Álgebra/Somatório/Fatorial-Demonstração
» Somatório Fatorial!
» Somatório fatorial
» Somatório
» Álgebra/Somatório/Fatorial-Demonstração
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












