(FUVEST) Função Trigonométrica
5 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
 (FUVEST) Função Trigonométrica
(FUVEST) Função Trigonométrica
O valor máximo da função =3.cos x+2.sen x) para
para  real é:
real é:
a)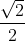 .
.
b)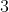 .
.
c)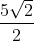 .
.
d)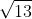 .
.
e)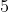 .
.
a)
b)
c)
d)
e)
- Spoiler:
- d)

ALDRIN- Membro de Honra

- Mensagens : 950
Data de inscrição : 29/07/2009
Idade : 41
Localização : Brasília-DF
 Re: (FUVEST) Função Trigonométrica
Re: (FUVEST) Função Trigonométrica
Eu já postei essa questão aqui no fórum, mas não acho :/ Até me lembro que está em meu livro de Ensino Médio, mas o mestre Euclides resolveu usando cálculo.

JoaoGabriel- Monitor

- Mensagens : 2344
Data de inscrição : 30/09/2010
Idade : 29
Localização : Rio de Janeiro
 Re: (FUVEST) Função Trigonométrica
Re: (FUVEST) Função Trigonométrica
Transcreve a resolução dele, por favor.

ALDRIN- Membro de Honra

- Mensagens : 950
Data de inscrição : 29/07/2009
Idade : 41
Localização : Brasília-DF
 Re: (FUVEST) Função Trigonométrica
Re: (FUVEST) Função Trigonométrica
Vc pode usar o 'truque' do triângulo retângulo:
Sendo a e b reais, existe theta tal que asenx + bcosx = sqrt(a²+b²) senx + theta
f(x) = 3cosx + 2senx
f(x) = sqrt(3²+2²) senx + theta
f(x) = sqrt(13)senx + theta
a função assume o valor máximo qdo x=90º, assim máx = V13
Tem a demonstração dessa fórmula na minha apostila, daqui a pouco eu posto pq meu word e firefox n estao abrindo, aí n da pra digitar os símbolos...
Sendo a e b reais, existe theta tal que asenx + bcosx = sqrt(a²+b²) senx + theta
f(x) = 3cosx + 2senx
f(x) = sqrt(3²+2²) senx + theta
f(x) = sqrt(13)senx + theta
a função assume o valor máximo qdo x=90º, assim máx = V13
Tem a demonstração dessa fórmula na minha apostila, daqui a pouco eu posto pq meu word e firefox n estao abrindo, aí n da pra digitar os símbolos...

Luck- Grupo
Velhos amigos do Fórum
- Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 32
Localização : RJ
 Re: (FUVEST) Função Trigonométrica
Re: (FUVEST) Função Trigonométrica

Demonstração:
Veja que:
Como
e

Luck- Grupo
Velhos amigos do Fórum
- Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 32
Localização : RJ
 Re: (FUVEST) Função Trigonométrica
Re: (FUVEST) Função Trigonométrica
Solução por derivadas
f(x) = 3cosx + 2senx
f '(x) = - 3senx + 2cosx
Para ser máximo f '(x) = 0 ----> - 3senx + 2cosx = 0 ----> 3senx = 2cos ----> 9sen²x = 4cos²x ----> 9sen²x = 4*(1 - sen²x) ----> 13sen²x = 4 --->
sen²x = 4/13 ----> senx = 2*\/13/13
cos²x = 1 - 4/13 ---> cos²x = 9/13 ----> cosx = 3*\/13/3
f(x)máx = 3*(3*\/13)/13) + 2*(2*\/13)/13 ----> f(x)máx = 9*\/13/13 + 4*\/13/13 ----> f(x)máx = \/13
f(x) = 3cosx + 2senx
f '(x) = - 3senx + 2cosx
Para ser máximo f '(x) = 0 ----> - 3senx + 2cosx = 0 ----> 3senx = 2cos ----> 9sen²x = 4cos²x ----> 9sen²x = 4*(1 - sen²x) ----> 13sen²x = 4 --->
sen²x = 4/13 ----> senx = 2*\/13/13
cos²x = 1 - 4/13 ---> cos²x = 9/13 ----> cosx = 3*\/13/3
f(x)máx = 3*(3*\/13)/13) + 2*(2*\/13)/13 ----> f(x)máx = 9*\/13/13 + 4*\/13/13 ----> f(x)máx = \/13

Elcioschin- Grande Mestre

- Mensagens : 73176
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: (FUVEST) Função Trigonométrica
Re: (FUVEST) Função Trigonométrica
Olá pessoal,
Uma outra solução ainda mais simples seria usar a desigualdade de Cauchy-Schwarz:
f(x) = 3cosx + 2senx
3cosx + 2senx = w
w² <= (3² + 2²)(cos²x + sen²x)
w² <= 9 + 4
w² <= 13
Como queremos o valor máximo:
w = V13
Uma outra solução ainda mais simples seria usar a desigualdade de Cauchy-Schwarz:
f(x) = 3cosx + 2senx
3cosx + 2senx = w
w² <= (3² + 2²)(cos²x + sen²x)
w² <= 9 + 4
w² <= 13
Como queremos o valor máximo:
w = V13
 Tópicos semelhantes
Tópicos semelhantes» Fuvest - função trigonométrica
» (Simulado FUVEST) Função trigonométrica
» (Fuvest-SP) expressão trigonométrica
» (FUVEST) Equação Trigonométrica
» Fuvest - equação trigonométrica
» (Simulado FUVEST) Função trigonométrica
» (Fuvest-SP) expressão trigonométrica
» (FUVEST) Equação Trigonométrica
» Fuvest - equação trigonométrica
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












