Desafio geométrico
2 participantes
Página 2 de 2
Página 2 de 2 •  1, 2
1, 2
 Desafio geométrico
Desafio geométrico
Relembrando a primeira mensagem :
Problema da trajetória
Seja ABC um triângulo isósceles com 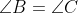 . A bissetriz do ângulo B intersecta o lado AC no ponto P. Suponha que a base BC permaneça fixa, mas a altura |AM| do triângulo tenda a 0, de forma que A tenda ao ponto médio M de BC. O que acontece com o ponto P durante esse processo?
. A bissetriz do ângulo B intersecta o lado AC no ponto P. Suponha que a base BC permaneça fixa, mas a altura |AM| do triângulo tenda a 0, de forma que A tenda ao ponto médio M de BC. O que acontece com o ponto P durante esse processo?
Problema da razão
Determinar a razão BP/PC no limite  , ou seja,
, ou seja,  .
.
Aqui temos dois problemas em um. A solução do primeiro leva diretamente à solução do segundo, logo tudo pode (e deve) ser visto como uma única situação em que o vértice A se desloca e o ponto P, por causa disso, descreve uma certa trajetória.
Divirtam-se.

gilberto97- Fera

- Mensagens : 590
Data de inscrição : 12/03/2014
Idade : 27
Localização : São Luís, Maranhão, Brasil
 Re: Desafio geométrico
Re: Desafio geométrico
Por acaso o valor da razão é 2? :scratch:
____________________________________________
"Death is so terribly final, while life is full of possibilities." - Tyrion Lannister
 Re: Desafio geométrico
Re: Desafio geométrico
Ahh, não tinha visto.
____________________________________________
"Death is so terribly final, while life is full of possibilities." - Tyrion Lannister
 Re: Desafio geométrico
Re: Desafio geométrico
A razão já foi encontrada. Parabéns 
Sobre a trajetória de P, darei uma dica.
É interessante imaginar os vértices do triângulo como sendo pontos no plano cartesiano R². O ponto P será a intersecção das retas BP e AC.
Sobre a trajetória de P, darei uma dica.
É interessante imaginar os vértices do triângulo como sendo pontos no plano cartesiano R². O ponto P será a intersecção das retas BP e AC.

gilberto97- Fera

- Mensagens : 590
Data de inscrição : 12/03/2014
Idade : 27
Localização : São Luís, Maranhão, Brasil
 Re: Desafio geométrico
Re: Desafio geométrico
Tem certeza? Talvez um pouco de "visão além do alcance" faça você mudar de ideia. De qualquer modo, postarei a minha resolução mais tarde. Obrigado por tentar resolver o desafio, RioBrancoabc.

gilberto97- Fera

- Mensagens : 590
Data de inscrição : 12/03/2014
Idade : 27
Localização : São Luís, Maranhão, Brasil
 Re: Desafio geométrico
Re: Desafio geométrico
Não adianta ter longo alcance como alguns mas não ter a artilharia como eu.
Convidado- Convidado
 Re: Desafio geométrico
Re: Desafio geométrico
O certo é ter os dois 
Como prometido, deixo minha resolução para os interessados.
Como prometido, deixo minha resolução para os interessados.
- Resolução:

Sejam,
e
os vértices do triângulo mencionado. Seja
o ponto médio de BC. Pelo gráfico acima, temos que
.
, pois o ângulo deve estar no primeiro quadrante.
Equação de BP:
Equação de AC:
A única variável envolvida é o "h", que tende a zero. É viável então "eliminá-lo". Como o ponto P é a intersecção entre AC e BP, pode-se isolar h em AC e jogar em BP.
y = 0 seria absurdo. Então as coordenadas de P satisfazem a equação
Concluímos que o ponto P descreve uma hipérbole (figura) quando o vértice A tende ao ponto médio M da base BC. Note que, pela dependência entre h e y, quando h->0, y->0, logo a equação da trajetória de P é reduzida para.
A escolha óbvia é x = 2a/3. Nessa situação, em que xP -> 2a/3, BP -> 2a/3 e PC -> a/3, logo a razão BP/PC tende a 2.

gilberto97- Fera

- Mensagens : 590
Data de inscrição : 12/03/2014
Idade : 27
Localização : São Luís, Maranhão, Brasil
 Re: Desafio geométrico
Re: Desafio geométrico
Até as coordenadas de P eu cheguei, mas não pensei em isolar o h...
Bem bacana!
Bem bacana!
____________________________________________
"Death is so terribly final, while life is full of possibilities." - Tyrion Lannister
Página 2 de 2 •  1, 2
1, 2
Página 2 de 2
Permissões neste sub-fórum
Não podes responder a tópicos













