Desafio geométrico

por **gilberto97** Dom 09 Abr 2017, 00:57

Problema da trajetória

Seja ABC um triângulo isósceles com 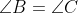$Desafio geométrico Gif$ . A bissetriz do ângulo B intersecta o lado AC no ponto P. Suponha que a base BC permaneça fixa, mas a altura |AM| do triângulo tenda a 0, de forma que A tenda ao ponto médio M de BC. O que acontece com o ponto P durante esse processo?

Problema da razão

Determinar a razão BP/PC no limite $Desafio geométrico Gif$ , ou seja, $Desafio geométrico Gif$ .

Aqui temos dois problemas em um. A solução do primeiro leva diretamente à solução do segundo, logo tudo pode (e deve) ser visto como uma única situação em que o vértice A se desloca e o ponto P, por causa disso, descreve uma certa trajetória.

Divirtam-se.

por **gilberto97** Qua 12 Abr 2017, 19:27

por Convidado Qua 12 Abr 2017, 20:00

Eu cheguei em PC=BC/3. Acho que está errado.

por **gilberto97** Qua 12 Abr 2017, 20:07

Apresente seu raciocínio.

por Convidado Qua 12 Abr 2017, 20:19

Fiz o teorema das bissetrizes; e fui reduzindo até deixar tudo em função de BC AM e PC. Agora não tenho tempo para colocar o raciocínio.
Desafio geométrico 20170411

Mas fiz no geogebra e deu isso mesmo.
Bate com o gabarito?

por **gilberto97** Qua 12 Abr 2017, 20:31

No limite em que A -> M, PC = BC/3, logo a razão BP/PC pedida é igual a 2 pois

BP = 2BC/3 e PC = BC/3.

No entanto, o problema pede a trajetória do ponto P à medida que A move-se em direção a M.