Pirâmides
3 participantes
Página 1 de 1
Pirâmides
por jhhj234 Sex 31 Mar 2017, 18:48
Uma pirâmide tem base quadrada e suas faces laterais são triângulos equiláteros de lado 10 cm. A altura dessa pirâmide, em cm, é
a) 5√3 b) 5√2 c) 3√3 d) 3√2
Gabarito:B
Gostaria de saber onde eu estou errando
Minha resolução:Apótema da base: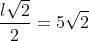
Como é um triangulo equilátero: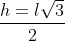
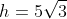
Agora aplicando Pitágoras com os valores encontrados: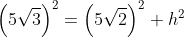
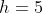
a) 5√3 b) 5√2 c) 3√3 d) 3√2
Gabarito:B
Gostaria de saber onde eu estou errando
Minha resolução:Apótema da base:
Como é um triangulo equilátero:
Agora aplicando Pitágoras com os valores encontrados:
jhhj234- Mestre Jedi
- Mensagens : 517
Data de inscrição : 05/04/2016
Idade : 25
Localização : RJ
Sam+uel gosta desta mensagem
Re: Pirâmides
por Elcioschin Sex 31 Mar 2017, 21:28
O apótema da base (quadrada) vale 10/2 = 5
Diagonal da base: D² = 10² + 10² ---> D² = 200
Distância do centro da base a um dos vértices da base = d = D/2 --> d² = D²/4 --> d² = 50
h² = 10² - d² ---> h² = 100 - 50 ---> h² = 50 ---> h = 5.√2
Diagonal da base: D² = 10² + 10² ---> D² = 200
Distância do centro da base a um dos vértices da base = d = D/2 --> d² = D²/4 --> d² = 50
h² = 10² - d² ---> h² = 100 - 50 ---> h² = 50 ---> h = 5.√2
Elcioschin- Grande Mestre
- Mensagens : 73163
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Sam+uel gosta desta mensagem
Re: Pirâmides
por ivomilton Sex 31 Mar 2017, 22:02
Boa noite, jhjh234.jhhj234 escreveu:Uma pirâmide tem base quadrada e suas faces laterais são triângulos equiláteros de lado 10 cm. A altura dessa pirâmide, em cm, é
a) 5√3 b) 5√2 c) 3√3 d) 3√2
Gabarito:B
Gostaria de saber onde eu estou errando
Minha resolução:Apótema da base:
Como é um triangulo equilátero:
Agora aplicando Pitágoras com os valores encontrados:
Note que BC = metade da diagonal do quadrado, e a altura é o outro cateto do triângulo ABC.
Alternativa (B)
Um abraço.
ivomilton- Membro de Honra
- Mensagens : 4994
Data de inscrição : 08/07/2009
Idade : 92
Localização : São Paulo - Capital
Sam+uel gosta desta mensagem
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
