Paridade de Função

por GFMCarvalho Seg 20 Mar 2017, 18:43

Boa noite, meus caros. Um amigo fez uma prova de cálculo I, e caiu o assunto de funções, e essa questão eu achei particularmente interessante, pois não consegui prová-la ainda:

Verifique se função é par, ímpar ou nenhuma das duas:

f(x)=\dfrac{x}{3^x-1}+\dfrac{x}{2}

Em todas minhas tentativas, deram cálculos de mais de uma página sem chegar em algo conclusivo, porém, para conferir, usei o Wolfram, o qual concluiu que a função era deveras par. Gostaria de alguma sugestão, já que apenas trocar x por -x não deu muito certo para mim Shocked

. Se alguém conseguir, compartilhe o raciocínio! Muito obrigado pela paciência! Very Happy

por leon030299 Seg 20 Mar 2017, 21:29

por já saber a resposta começarei pela prova de que f(x) é função par.

verificamos se há simetria na função quanto ao eixo Y e para isso f(x)=f(-x).
supomos isso,portanto:
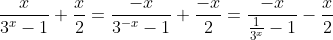
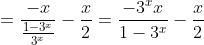$Paridade de Função Gif$
$Paridade de Função Gif$ então temos,olhando para o inicio da fila:
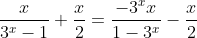$Paridade de Função Gif$ daí:
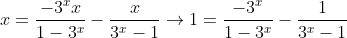$Paridade de Função Gif$ por motivos didáticos 3^x=t:

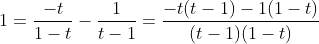$Paridade de Função Gif$ portanto:
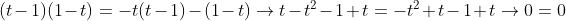$Paridade de Função Gif$ o que é verdadeiro. verdadeiro em que? em supor que há simetria na função quanto ao eixo Y(ou paridade,como queira).