questao do simulado do Elite

por **Bruna Barreto** Qua 13 Abr 2011, 22:08

Determine quantos numeros naturais menores que 2011 tem um numero ímpar de divisores positivos.
a)1005
b)502
c)105
d)80
e)44
bom o professor fez de um jeito e eu nao entendi a resposta é letra e)
por favor seja claro nos calculos....espero entender aqui Laughing

por **Elcioschin** Qui 14 Abr 2011, 09:02

Basta checar todos os expoentes pares

2^2 tem 3 divisores ----> 1, 2, 4
2^4 tem 5 divisores ----> 1, 2, 4, 8, 16
E assim por diante 2^n para n par tem número ímpar de divisores ---> 2048 = 2^20 ----> n = 10

3^6 = 729 ----> n = 3

5^4 = 625 ----> n = 2

6^4 = 216 ----> n = 2

7^4 = 343 -----> n = 2

10^2 = 100 ----> n = 1

11^2 = 121 ----> n = 1

12^2 = 144 -----> n = 1

13^2 = 169 ----> n = 1

14^2 = 196 ----> n = 1

15^2 = 225 ----> n = 1

17^2 = 289 ----> n = 1

E assim por diante, até 45^2 = 2025, evitando 25², 27², 36², pois já foram considerados anteriormente

Depois basta contar os vermelhos

por **abelardo** Qui 14 Abr 2011, 11:43

Há uma técnica, ou fórmula mesmo, para determinação da quantidade de divisores de qualquer número. Consiste no seguinte: ''Fatoramos o número e pega-se os expoentes de todos os fatores primos da decomposição, depois somamos $1$ a cada expoente e multiplicamos os novos expoentes, um pelo outro. Ex: $6=2\cdot 3 \to 2^1\cdot 3^1 \rightarrow (1+1).(1+1)=4$ , logo seis tem quatro divisores (1,2,3 e 6).

A questão pede para descobrir quantos numeros naturais menores que 2011 tem um numero ímpar de divisores positivos. Percebi a ideia da questão depois que fiz o seguinte --> imaginei um número qualquer, chamei-o de $N$ , logo fatorando-o terei o seguinte $\emph{N=}A^a\cdot B^b\cdot C^c\cdot D^d ...$ , o número de divisores de N é igual a: $(a+1)\cdot (b+1)\cdot (c+1)\cdot (d+1)...$ se os expoentes forem números pares, terei como resultado um número ímpar, mas se os expoentes forem ímpares terei como resultado um número par. Logo a, b, c, d ... são números pares.

Eu parei nessa parte e vi que poderia colocar vários números de várias formas, logo fiz algumas multiplicações de fatores primos (cada um elevado a um número par) e vi que os números que atendem a questão são quadrados perfeitos (Achei cômico)! O maior quadrado perfeito menor que 2011 é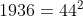 $1936=44^2$ . Tenho 44 quadrados perfeitos até 1936, logo tenho 44 números menores que 2011 com uma quantidade ímpar de divisores positivos!

por **Bruna Barreto** Qui 14 Abr 2011, 23:06

GENTE NAO ENTENDI NADA..TO MUITO CONFUSA NESSA PARTE NAO SEI essa parte de quantidade impar nao to conseguindo entender

por **abelardo** Sex 15 Abr 2011, 15:07

Separemos a questão para que fique mais clara --> Determine quantos números naturais menores que 2011 tem um número ímpar de divisores positivos. Dividi a questão em duas partes. A partir da vermelha podemos concluir que 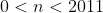$0 < n < 2011$ . A condição de existência desses números é que tenham uma ''quantidade'' (Número) ÍMPAR de divisores. Para responder a parte de azul, você deve saber, antes de qualquer outra coisa, que para determinar a quantidade de divisores de qualquer número inteiro positivo há uma técnica simples e que já expliquei ( Fatora o número, pega o(s) expoente(s) da(s) potência(s) final(is), soma a unidade a cada e multiplica-se uma por outra... se você não entendeu ainda essa parte, pesquisa na net ''quantidade de divisores de um número''). Aqui acredito que você já tenha dominado a técnica para determinar a quantidade de divisores de um número inteiro positivo. Veja que podemos generalizar as coisas da seguinte maneira -->

Qualquer número fatorado ficará da seguinte forma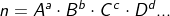 $\fn_cm n= A^a \cdot B^b \cdot C^c\cdot D^d ...$

Para determinar a quantidade de divisores de qualquer número teremos $\dpi{100} \fn_cm Q$ $\dpi{80} \fn_cm (d)$ $\dpi{100} \fn_cm = (a + 1)\cdot (b+1)\cdot (c+1)\cdot (d+1)...$

Sabendo disso e lembrando que a questão quer saber quantos são os números com uma quantidade de divisores ímpares, devemos então pensar ''para que um número tenha uma quantidade de divisores ímpares, usando a fórmula para determinar a quantidade de divisores, posso eu perceber algum padrão nesses números?''. Lembre-se que um número ímpar é resultado da multiplicação de um número ímpar por outro, então $\dpi{100} \fn_cm = (a + 1)\cdot (b+1)\cdot (c+1)\cdot (d+1)...$ são fatores ímpares, logo $\dpi{100} \fn_cm a,b,c,d ...$ são todos números pares.

Quando cheguei a esse ponto da questão fiquei pensando ''poh véio, existem vários números menores que 2011 que quando fatorados produzem fatores primos com expoentes pares...''. Então começei a fazer aleatoriamente alguns produtos com fatores primos elevados a expoentes pares e percebi que todos eles eram quadrados perfeitos e você pode testar isso. Bom, o maior quadrado perfeito menor que 2011 é 1936. Veja isso:
$\dpi{100} \fn_cm 1936 = 2^4 \cdot 11^2$
$\dpi{100} \fn_cm 1849 = 43^2$
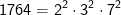
$\dpi{100} \fn_cm 1764 = 2^2 \cdot 3^2 \cdot 7^2$
$\dpi{100} \fn_cm 1681= 41^2$
$\dpi{100} \fn_cm 1600= 2^6 \cdot 5^2$
...........
...........
...........
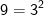
$\dpi{100} \fn_cm 9= 3^2$
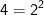
$\dpi{100} \fn_cm 4= 2^2$
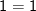$\dpi{100} \fn_cm 1= 1$ (O número um apresenta somente um divisor, a quantidade de divisores de 1 é igual a 1 e esse número é impar, ele completa a lista dos 44 números).

Qualquer dúvida, pode perguntar, não se achanhe.