Função seno-FME
3 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Função seno-FME
por XablauTOMrafa1 Dom 05 Mar 2017, 14:20
Alguém pode me ajudar com essa questão ?
Para que valores de M existe x que satisfazendo a igualdade Sen X = (m-1)/(m-2)
gab M<3/2
Para que valores de M existe x que satisfazendo a igualdade Sen X = (m-1)/(m-2)
gab M<3/2
XablauTOMrafa1- Iniciante
- Mensagens : 33
Data de inscrição : 04/12/2016
Idade : 28
Localização : cariacicaES
Re: Função seno-FME
por Elcioschin Dom 05 Mar 2017, 15:33
-1 ≤ senx ≤ 1 ---> -1 ≤ (m - 1).(m - 2) ≤ 1
Desenvolva a função no meio.
Separe em duas inequações.
Determine o domínio (intervalos) da função de cada inequação.
Determine a interseção dos dois domínios.
Desenvolva a função no meio.
Separe em duas inequações.
Determine o domínio (intervalos) da função de cada inequação.
Determine a interseção dos dois domínios.
Elcioschin- Grande Mestre
- Mensagens : 73176
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
XablauTOMrafa1- Iniciante
- Mensagens : 33
Data de inscrição : 04/12/2016
Idade : 28
Localização : cariacicaES
Re: Função seno-FME
por Zaqueu Dom 05 Mar 2017, 15:49
Olá.
O seno de qualquer ângulo varia entre -1 e 1. Logo -1 ≤ (m-1)/(m-2) ≤ 1
I) (m-1)/(m-2) ≥ -1
(m-1)/(m-2) + 1 ≥ 0
(m-1)/(m-2) + (m-2)/m-2 ≥ 0
(2m-3)/(m-2) ≥ 0
Numerador positivo ---> m > 3/2 |
Denominador positivo ---> m > 2 |---> m > 2
Numerador negativo ---> m < 3/2 |
Denominador negativo ---> m < 2 |---> m < 3/2
(2m-3)/(m-2) = 0 ---> m = 3/2
Assim, os valores que m deve assumir são: (união dos intervalos acima)
II) (m-1)/(m-2) ≤ 1
(m-1)/(m-2) - 1 ≤ 0
(m-1)/(m-2) - (m-2)/(m-2) ≤ 0
1/(m-2) ≤ 0 m ≠ 2
(m-2) < 0
m < 2
-------------------------------------------------------------------
Fazendo a interseção entre os valores que m precisa assumir:
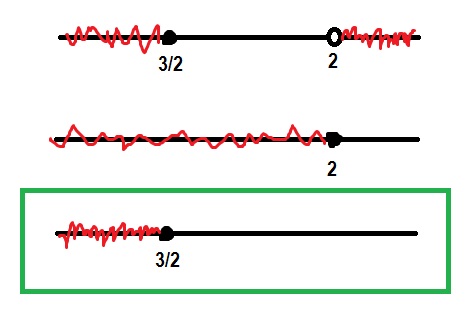
O seno de qualquer ângulo varia entre -1 e 1. Logo -1 ≤ (m-1)/(m-2) ≤ 1
I) (m-1)/(m-2) ≥ -1
(m-1)/(m-2) + 1 ≥ 0
(m-1)/(m-2) + (m-2)/m-2 ≥ 0
(2m-3)/(m-2) ≥ 0
Numerador positivo ---> m > 3/2 |
Denominador positivo ---> m > 2 |---> m > 2
Numerador negativo ---> m < 3/2 |
Denominador negativo ---> m < 2 |---> m < 3/2
(2m-3)/(m-2) = 0 ---> m = 3/2
Assim, os valores que m deve assumir são: (união dos intervalos acima)
II) (m-1)/(m-2) ≤ 1
(m-1)/(m-2) - 1 ≤ 0
(m-1)/(m-2) - (m-2)/(m-2) ≤ 0
1/(m-2) ≤ 0 m ≠ 2
(m-2) < 0
m < 2
-------------------------------------------------------------------
Fazendo a interseção entre os valores que m precisa assumir:
Zaqueu- Recebeu o sabre de luz
- Mensagens : 170
Data de inscrição : 25/05/2014
Idade : 26
Localização : Caruaru, PE, Brasil
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
