Soma vetorial

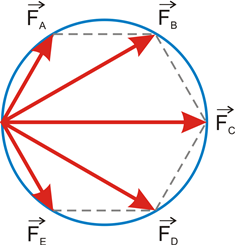
A figura mostra 5 forças representadas por vetores de origem comum, dirigindo-se aos vértices de um hexágono regular. Sendo 10N o módulo da força Fc, a itensidade resultante dessas 5 forças é: 


a) 50N
b) 45N 
c) 40N
d) 35N 
e) 30N


Alguém pode explicar essa resolução? Ou dar uma solução através do hexágono formado

Para facilitar vou chamar de F = Fa = Fe e de F' = Fb = Fd
Seja O o ponto de origem das forças:

No triângulo isósceles FaOFb ---> F' =  2.F.cos30º ---> F' = F.√3 ---> F'² = 3.F²

No triângulo retângulo  OFbFc ---> (Fb)² + (FbFc)² = Fc² ---> F'² + F²  = 10² ---> 3.F² + F² = 100 --->

4.F² = 100 ---> F² = 25 ---> F = 5 ---> F' = 5.√3

R = 2.F.cos60º + 2.F'.cos30º + Fc ---> R² = 2.5.(1/2) + 2.(5.√3).(V3/2) + 10 ---> R = 30 N

Vou fazer de outro modo:

Note que:

F_C=F_A+F_D e F_C=F_B+F_E

F_Resultante=F_A+F_B+F_C+F_D+F_E=(F_A+F_D)+F_C+(F_B+F_E)=F_C+F_C+F_C=3F_C

F_C=10 N -> F_Resultante=3.10=30 N

Muito obrigado pela solução, Giovana. Mas teria alguma forma de se resolver através do hexágono regular? Se "apropriando" da geometria?

Um jeito utilizando geometria e trigonometria:

No ∆MOP -> cos 30°=F_B/F_C -> √3/2=F_B/10 -> F_B=F_D=5√3 N

(F_BD)²=(F_B)²+(F_D)²+2.F_B.F_D.cos 60° -> F_BD=15 N

No ∆MNP -> cos 60°=F_A/F_C -> 1/2=F_A/10 -> F_A=F_E=5 N

Como o ângulo entre F_A e F_E mede 120°, a resultante entre essas forças (F_AE) equivale também 5 N.

F_R=F_C+F_AE+F_BD=10+5+15=30 N

Muito obrigado, Giovana! Suas soluções são sempre ótimas!!!

Muito obrigada !!