Hexágono OBM

O Hexágono ABCDEF é circunscritível . Se AB = 1 , BC = 2 , CD = 3 , DE = 4 EF=5 , quanto mede FA ?

 

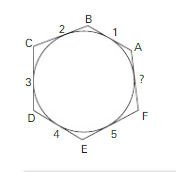
a) 1 b) 3 c)15/8 d)6 e)9

[img][/img]

Matemathiago escreveu:" />

Ficou um pouco difícil enxergar as resoluções mas obrigado.

Os raios em vermelho da circunferência formam 90 graus com os lados. Entre dois desses lados consecutivos há sempre dois seguimentos do hexágono que são sempre congruentes. Por isso as letras se repetem conforme o desenho.

Como na imagem da questão temos os valores de 5 lados, podemos montar um sistema conforme abaixo, sempre comparando as letras do desenho que eu fiz com os valores na imagem da questão.

Do desenho:

x+k = 1
x + t = 2
t+ w = 3
w + z = 4
z + m = 5

Somando tudo do lado esquerdo e tudo do lado direito:
2x + 2t + 2w + 2z + m + k = 1+2+3+4+5
2(x+t) + 2(w+z) + m+k = 15
2(2) + 2(4) + m + k = 15
4+8+m+k = 15
12 + m + k = 15
m + k = 3

Como m + k = AF:

AF = 3

Espero que tenha facilitado!

Matemathiago escreveu:Os raios em vermelho da circunferência formam 90 graus com os lados. Entre dois desses lados consecutivos há sempre dois seguimentos do hexágono que são sempre congruentes. Por isso as letras se repetem conforme o desenho.

Como na imagem da questão temos os valores de 5 lados, podemos montar um sistema conforme abaixo, sempre comparando as letras do desenho que eu fiz com os valores na imagem da questão.

Do desenho:

x+k = 1
x + t = 2
t+ w = 3
w + z = 4
z + m = 5

Somando tudo do lado esquerdo e tudo do lado direito:
2x + 2t + 2w + 2z + m + k = 1+2+3+4+5
2(x+t) + 2(w+z) + m+k = 15
2(2) + 2(4) + m + k = 15
4+8+m+k = 15
12 + m + k = 15
m + k = 3

Como m + k = AF:

AF = 3

Espero que tenha facilitado!

Obrigado.

Disponha!