Semelhança
2 participantes
Página 1 de 1
Semelhança
por lucasconrado Seg 07 Nov 2016, 23:50
(UE-CE) A circunferência da figura tem centro no ponto O e M é o ponto de interseção das cordas P1P2 e Q1Q2. Se P1M = 4 cm, MP2 = (k + 1) cm, Q1M = 3 cm e MQ2 = (3k – 7) cm, então a corda Q1Q2 , em cm , mede:
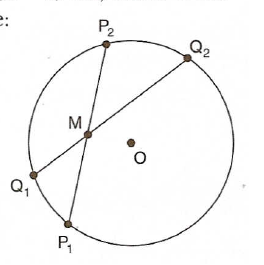
a)5
b)8
c)11
d)14
Obs:. Não tenho o gabarito.
a)5
b)8
c)11
d)14
Obs:. Não tenho o gabarito.
lucasconrado- Jedi
- Mensagens : 262
Data de inscrição : 13/07/2016
Idade : 32
Localização : RJ
Re: Semelhança
por Elcioschin Ter 08 Nov 2016, 00:10
4.(k + 1) = 3.(3.k - 7) ---> 4.k + 4 = 9.k - 21 ---> k = 5
Q1Q2 = Q1M + MQ2 = 3 + (3.k - 7) = 3 + (3.5 - 7) = 11
Q1Q2 = Q1M + MQ2 = 3 + (3.k - 7) = 3 + (3.5 - 7) = 11
Elcioschin- Grande Mestre
- Mensagens : 73174
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Semelhança
por lucasconrado Ter 08 Nov 2016, 00:12
Elcio, eu queria entender o porque esses triângulos são semelhantes. Não consegui enxergar a semelhança entre eles.
lucasconrado- Jedi
- Mensagens : 262
Data de inscrição : 13/07/2016
Idade : 32
Localização : RJ
Re: Semelhança
por Elcioschin Ter 08 Nov 2016, 00:14
Não existe nenhum triângulo na figura!!!! Logo não existe semelhança de triângulos.
Estude a teoria: Cordas numa circunferência
Estude a teoria: Cordas numa circunferência
Elcioschin- Grande Mestre
- Mensagens : 73174
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Semelhança
por lucasconrado Ter 08 Nov 2016, 00:17
Essa questão estava no modulo de semelhança de triângulos, por isso pensei tentei resolvê-lá por semelhança. Vou dar um olhada nessa matéria. Obrigado
lucasconrado- Jedi
- Mensagens : 262
Data de inscrição : 13/07/2016
Idade : 32
Localização : RJ
Re: Semelhança
por Elcioschin Ter 08 Nov 2016, 08:41
lucasconrado
O nome correto do assunto é "Relações Métricas na Circunferência"
Teorema 1: Se duas cordas AB e CD de uma circunferência concorrem num ponto P interior da mesma, então: PA.PB = PC.PD
A demonstração deste teorema se baseia em três outros teoremas:
A^PD = B^PC ---> opostos pelo vértice
BÂD = B^CD ---> ângulos internos que subentendem o mesmo arco BD
∆ APD ~ ∆ BPC ---> semelhança de triângulos
O nome correto do assunto é "Relações Métricas na Circunferência"
Teorema 1: Se duas cordas AB e CD de uma circunferência concorrem num ponto P interior da mesma, então: PA.PB = PC.PD
A demonstração deste teorema se baseia em três outros teoremas:
A^PD = B^PC ---> opostos pelo vértice
BÂD = B^CD ---> ângulos internos que subentendem o mesmo arco BD
∆ APD ~ ∆ BPC ---> semelhança de triângulos
Elcioschin- Grande Mestre
- Mensagens : 73174
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
