Binômio de Newton

por Legendcross Dom 23 Out 2016, 09:33

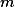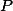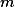Escreva o desenvolvimento do binômio $Binômio de Newton Mathtex$ , onde $Binômio de Newton Mathtex$ é um número inteiro maior que zero, em termos de potências inteiras de $Binômio de Newton Mathtex$ e $Binômio de Newton Mathtex$ . Para determinados valores do expoente, este desenvolvimento possuirá uma parcela $Binômio de Newton Mathtex$ , que não conterá a função $Binômio de Newton Mathtex$ . Seja $Binômio de Newton Mathtex$ o menor valor para o qual isso ocorre. Então $Binômio de Newton Mathtex$ quando $Binômio de Newton Mathtex$ for igual a:

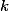a) $Binômio de Newton Mathtex$ , com $Binômio de Newton Mathtex$ inteiro

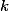b) $Binômio de Newton Mathtex$ , com $Binômio de Newton Mathtex$ inteiro

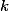c) $Binômio de Newton Mathtex$ , com $Binômio de Newton Mathtex$ inteiro

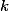d) $Binômio de Newton Mathtex$ , com $Binômio de Newton Mathtex$ inteiro

e) não existe $Binômio de Newton Mathtex$ satisfazendo a igualdade desejada

gab: d

Na resolução, chega-se a ''cos²x=3/4'',portanto cos x = ± $Binômio de Newton 3b19c09494138b5082459afac7f9a8d99c546fcd$ /2

Sendo assim, X pode ser 30º,150º,210º,330º e assim por diante

portanto x=±π/6 + kπ, o que não aparece em nenhuma alternativa.

Queria saber o que estou errando para chegar a essa conclusão ou se o gabarito está errado.

por EsdrasCFOPM Seg 24 Out 2016, 00:00

Eu não sei de onde você pegou essa fórmula, mas no livro que tenho aqui a equação do tipo cos x=cos α fica:

x=±α+2kπ, com k ∈ ℤ.

Binômio de Newton 11jm0zt

por Legendcross Qua 26 Out 2016, 19:37

Veja que no seu livro o autor delimita apenas o valor positivo do cosseno. O meu resultado deu cos x = ± $Binômio de Newton 3b19c09494138b5082459afac7f9a8d99c546fcd$ /2, ou seja, o cosseno pode ser tanto positivo quanto negativo.

por **Elcioschin** Qua 26 Out 2016, 19:48

Legendcrosss

Infelizmente você não postou a solução completa do seu livro: mostrou apenas a conclusão final cosx = ± √3/2

Caso esta solução esteja correta (não sabemos se está), o gabarito está errado. O correto é x = ± pi/6 + k.pi

Veja:

Para k = 0 ---> x = ± pi/6 (30º e 330º) ---> Solução válida para k par
Para k = 1 ---> x = ± pi/6 + pi (150º e 210º) ---> Solução válida para k ímpar

por Legendcross Qua 26 Out 2016, 21:51

A resolução é igual a essa :
Reescrevendo a expressão,
$Binômio de Newton Mathtex$

O termo P que não contém $Binômio de Newton Mathtex$ será quando
$Binômio de Newton Mathtex$
$Binômio de Newton Mathtex$

Assim temos
$Binômio de Newton Mathtex$
$Binômio de Newton Mathtex$
$Binômio de Newton Mathtex$
$Binômio de Newton Mathtex$ . Letra D