Teoria dos números (divisibilidade)
2 participantes
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Teoria dos números (divisibilidade)
por John von Neumann jr Dom 17 Jul 2016, 19:40
(Cone Sul 1996) Provar que o número [img]
[/img] é um inteiro.
Sol: [img]
[/img]
Não entendi a parte marcada em vermelho.
[/img] é um inteiro.Sol: [img]
[/img]Não entendi a parte marcada em vermelho.
John von Neumann jr- Jedi
- Mensagens : 350
Data de inscrição : 18/12/2015
Localização : Brasil
Re: Teoria dos números (divisibilidade)
por Ashitaka Seg 18 Jul 2016, 22:21
Ele pegou as duas parcelas da primeira linha e justificou que cada uma delas é um inteiro.
A parte em vermelho é a justificativa da primeira parcela.
Usando a fatoração do x^n - y^n em (1997^1996 - 1), você chega no termo que está no ( ) grande em vermelho.
A parte em vermelho é a justificativa da primeira parcela.
Usando a fatoração do x^n - y^n em (1997^1996 - 1), você chega no termo que está no ( ) grande em vermelho.
Ashitaka- Monitor
- Mensagens : 4365
Data de inscrição : 12/03/2013
Localização : São Paulo
Re: Teoria dos números (divisibilidade)
por John von Neumann jr Ter 19 Jul 2016, 13:07
A fatoração de 1997^1996 - 1 não seria:
?
?
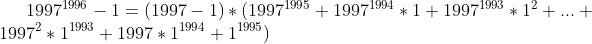
John von Neumann jr- Jedi
- Mensagens : 350
Data de inscrição : 18/12/2015
Localização : Brasil
Re: Teoria dos números (divisibilidade)
por Ashitaka Ter 19 Jul 2016, 18:41
É verdade, seria isso mesmo que você disse...
Ashitaka- Monitor
- Mensagens : 4365
Data de inscrição : 12/03/2013
Localização : São Paulo
Tópicos semelhantes» Teoria dos números - divisibilidade
» Teoria dos Números - Divisibilidade
» Teoria dos Números - Divisibilidade (?)
» Teoria dos números (divisibilidade)
» Teoria dos números (divisibilidade)
» Teoria dos Números - Divisibilidade
» Teoria dos Números - Divisibilidade (?)
» Teoria dos números (divisibilidade)
» Teoria dos números (divisibilidade)
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
