Equação da reta através da área do triângulo

Seja "O" a origem de um sistema de coordenadas cartesianas. Uma reta ''r'' corta os eixos coordenados em pontos ''A'' e ''B'' de modo que o triângulo AOB tem área igual a 20. Determine a equação de ''r'' sabendo que ela é perpendicular à reta de equação 
2x-5y+35=0.

R: 5x+2y+20=0   ou    5x+2y - 20=0

Sejam A( xA, 0 ) e B( 0, yB )

então temos:

( xA*yB )/2 = 20 -> xA*yB = 40 (I)



- reta (r):

2x - 5y + 35 = 0 -> y = ( 2/5 )*x + ( 7 ) -> coeficiente angula igual a :

m = - 5/2


- reta que passa pelos pontos A( xA, 0 ) e B( 0, yB ):

m' = - 5/2

( y - 0 )/( yB - 0 0 = ( X - XA )/(0 - xA ) -> y = ( yB/( - xA )*x + ( yB*xA )/( - xA )

coeficiente angular -> m'' = yB/(- xA ) = - 5/2 (II)


de (I) e (II) temos:

yB = ( 5/2 )*( 40/yB ) -> yB = (+/-) 10


- para yB = 10 -> xA = 4

- reta por A( 4, 0 ) e B( 0, 10 ) -> 5x + 2y - 20 = 0



- para yB = - 10 -> xA = - 4

- reta por A( - 4, 0 ) e B( 0, - 10 ) -> 5x + 2y + 20 = 0

Jose Carlos escreveu:Sejam A( xA, 0 ) e B( 0, yB )

então temos:

( xA*yB )/2 = 20 -> xA*yB = 40 (I)



- reta (r):

2x - 5y + 35 = 0 -> y = ( 2/5 )*x + ( 7 ) -> coeficiente angula igual a :

m = - 5/2


- reta que passa pelos pontos A( xA, 0 ) e B( 0, yB ):

m' = - 5/2

( y - 0 )/( yB - 0 0 = ( X - XA )/(0 - xA ) -> y = ( yB/( - xA )*x + ( yB*xA )/( - xA )

coeficiente angular -> m'' = yB/(- xA ) = - 5/2 (II)


de (I) e (II) temos:

yB = ( 5/2 )*( 40/yB ) -> yB = (+/-) 10


- para yB = 10 -> xA = 4

- reta por A( 4, 0 ) e B( 0, 10 ) -> 5x + 2y - 20 = 0



- para yB = - 10 -> xA = - 4

- reta por A( - 4, 0 ) e B( 0, - 10 ) -> 5x + 2y + 20 = 0

 Pessoal, alguém poderia esclarecer um pouco esta explicação? Fiquei um pouco perdido depois de achar o coeficiente angular.

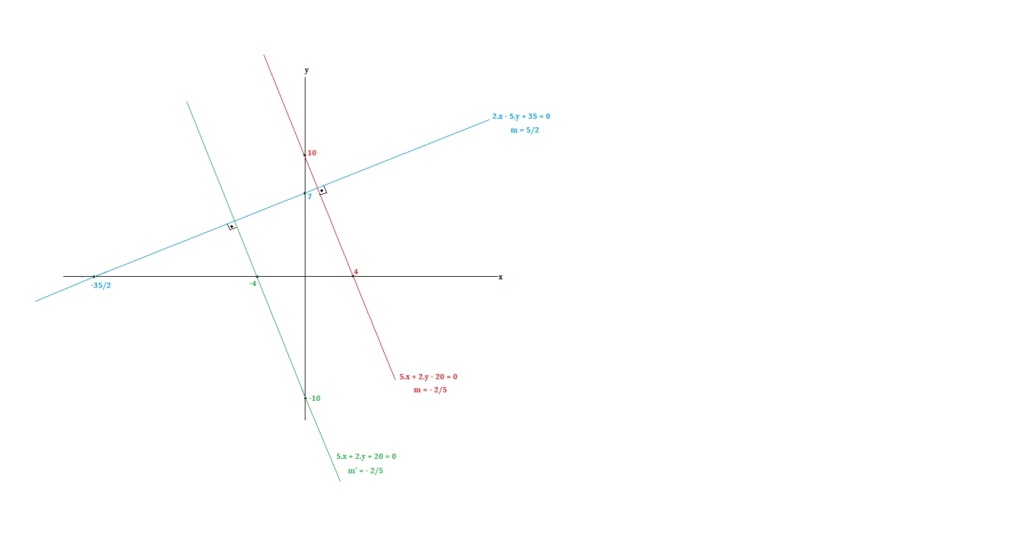
Reta perpendicular à reta procurada ---> 2.x - 5.y + 35 = 0 ---> y = (2/5).x + 7

Coeficiente angular desta reta ---> m = 2/5

Reta procurada passa por A(xA, 0) e B(0, yB) e tem m' = - 5/2

Área ---> xA.yB/2 = 20 ---> xA.yB = 40 ---> yB = 40/xA ---> I

- yB/xA = - 5/2 ---> yB = (5/2).xA ---> II

II = I ---> (5/2).xA = 40/xA ---> xA² = 16 ---> xA = ±­ 4


Para xA = + 4 ---> yA = + 10
Para xA = - 4 ----> yA = - 10

Elcioschin escreveu:Reta perpendicular à reta procurada ---> 2.x - 5.y + 35 = 0 ---> y = (-2/5).x + 7

Coeficiente angular desta reta ---> m = - 2/5

Reta procurada passa por A(xA, 0) e B(0, yB) e tem m' = 5/2

Área ---> xA.yB/2 = 20 ---> xA.yB = 40 ---> yB = 40/xA ---> I

- yB/xA = - 5/2 ---> yB = (5/2).xA ---> II

II = I ---> (5/2).xA = 40/xA ---> xA² = 16 ---> xA = ±­ 4


Para xA = + 4 ---> yA = + 10
Para xA = - 4 ----> yA = - 10

 Poderia por gentileza explicar como montou a equação II? Acho que entendi o princípio (a = ∆y/∆x), mas não entendi o fato do sinal negativo.
 
 Obrigado!

Eu digitei um sinal errado na equação da reta dada: o correto é y = (2/5).x + 7 (Já editei)
Note que o coeficiente angular dela é positivo (reta crescente)

Eu usei xA , yB em módulo.

Logo, qualquer reta perpendicular a ela tem coeficiente angular negativo: m = - 2/5 (reta decrescente): 

m = - yB/xA