Probabilidade e Análise Combinatória

por **Giovana Martins** 25/6/2016, 3:21 pm

5 homens e 5 mulheres compram 10 cadeiras consecutivas na mesma fila de um teatro. Supondo que se sentaram aleatoriamente nas 10 cadeiras, calcular:

A) A probabilidade de que homens e mulheres se sentem em cadeiras alternadas.
B) A probabilidade de que as mulheres se sentem juntas.

A) 1/126
B) 1/42

por **gilberto97** 25/6/2016, 5:03 pm

Boa tarde.

Homens e Mulheres em Cadeiras Alternadas:

HMHMHMHMHM ou MHMHMHMHMH

Total de maneiras: 10!

Assim:

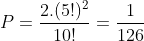
$Probabilidade e Análise Combinatória Gif.latex?P%20%3D%20%5Cfrac%7B2$

Mulheres Juntas:

MMMMMHHHHH ou HMMMMMHHHH ou HHMMMMMHHH ...

Perceba que podemos tratar as 5 mulheres como uma coisa só.

XHHHHH ou HXHHHH ou HHXHHH ou HHHXHH ou HHHHXH ou HHHHHX

São 6 maneiras. Então, para os homens existem 5! maneiras de se sentarem, para as mulheres 5! também (entre elas). Logo:

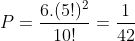
$Probabilidade e Análise Combinatória Gif.latex?P%20%3D%20%5Cfrac%7B6$

por ricardo.rad 26/6/2016, 11:41 am

A) Imaginando que as cadeiras estão numeradas de 1 a 10. Primeiro decidimos se as mulheres setaram nas cadeiras pares, ou nas cadeiras ímpares em seguida escolhemos a ordem em que as cinco se sentarão, P_5=5!, enfim a ordem em que os cinco homens sentarão P_5=5!.
Resposta: \dfrac{2\cdot(5!)^2}{10!}=\dfrac{1}{126}.

B) Pensamos nas cinco mulheres como um bloco único de pessoas então devemos permutar esse bloco e os cinco homens, P_6=6!, em seguida permutamos as mulheres no bloco, P_5=5!.
Resposta: \dfrac{6!\cdot5!}{10!}=\dfrac{1}{42}.