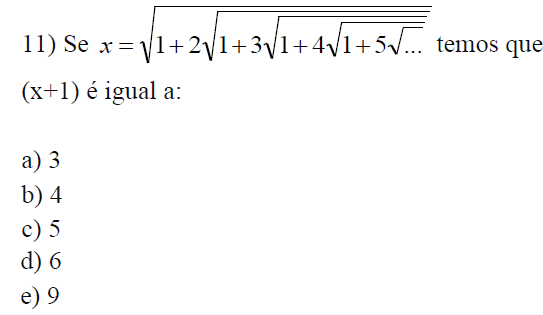Radiciação !!
+3
pxpc2
ivomilton
glauciomelo
7 participantes
Página 1 de 1

glauciomelo- Jedi

- Mensagens : 232
Data de inscrição : 28/02/2016
Idade : 25
Localização : Parnamirin,RN , Brasil
 Re: Radiciação !!
Re: Radiciação !!
Bom dia, Glaucio.
Está difícil para alguém resolver, sem saber de qual prova é, de que ano, de qual Escola Militar.
Se não tiver mesmo como saber a origem, a única saída será aguardar para ver se alguém aparece que saiba resolver.
O amigo de quem lhe falei não está conseguindo.
Um abraço.

ivomilton- Membro de Honra

- Mensagens : 4994
Data de inscrição : 08/07/2009
Idade : 92
Localização : São Paulo - Capital
 Re: Radiciação !!
Re: Radiciação !!
Deveria ser letra (B), como resolver sem ser por computacao nao sei, mas este é um dos clássicos problemas do matemático Ramanujan, você encontra bastante coisa a respeito na internet, como por exemplo o fato de que esta serie rapidamente converge para 3. Assim, teriamos 3 + 1 = 4.
 Re: Radiciação !!
Re: Radiciação !!
Brother! um colega respondeu a minha questão e aí mandei a sua pra ele.
Ele me mandou isso:

Atualizando:
Ele disse que sempre dá um valor aproximado, porque √... significa continuidade.Haverá infinitas raízes, chegando a um ponto em que o valor x passa de 3. Enfim, damos a reposta como 3 por aproximação.
Ele me mandou isso:

Atualizando:
Ele disse que sempre dá um valor aproximado, porque √... significa continuidade.Haverá infinitas raízes, chegando a um ponto em que o valor x passa de 3. Enfim, damos a reposta como 3 por aproximação.

Arley Motta- Jedi

- Mensagens : 210
Data de inscrição : 27/05/2016
Idade : 28
Localização : Bahia, Brasil
 Re: Radiciação !!
Re: Radiciação !!
Isto não é sempre verdade
Eis um exemplo em que dá para calcular exato:
x = √{2 + √[2+ √(2 + √....]} ---> infinitos radicais, somente com o número 2
Elevando ao quadrado:
x² = 2 + √[2+ √(2 + ....] ---> a última parcela é igual a x, já que são infinitos radicais:
x² = 2 + x
x² - x - 2 = 0 ---> Raiz positiva ---> x = 2
Eis um exemplo em que dá para calcular exato:
x = √{2 + √[2+ √(2 + √....]} ---> infinitos radicais, somente com o número 2
Elevando ao quadrado:
x² = 2 + √[2+ √(2 + ....] ---> a última parcela é igual a x, já que são infinitos radicais:
x² = 2 + x
x² - x - 2 = 0 ---> Raiz positiva ---> x = 2

Elcioschin- Grande Mestre

- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Radiciação !!
Re: Radiciação !!
Observe
n^2=n^2-1+1
n^2=(n-1)(n+1)+1
n^2=1+(n-1)(n+1)
Então
3^2=1+2\cdot4 \Rightarrow 3=\sqrt{1+2\cdot4}
4^2=1+3\cdot5 \Rightarrow 4=\sqrt{1+3\cdot5}
5^2=1+4\cdot6 \Rightarrow 5=\sqrt{1+4\cdot6}
6^2=1+5\cdot7 \Rightarrow 6=\sqrt{1+5\cdot7}
\vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots
então
3=\sqrt{1+2\cdot4}
3=\sqrt{1+2\sqrt{1+3\cdot5}}
3=\sqrt{1+2\sqrt{1+3\sqrt{1+4\cdot6}}}
3=\sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{1+5\cdot7}}}}
3=\sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{1+5\sqrt{\cdots}}}}}
Assimx=3 e x+1=4
Então
então
Assim
poisedom- Padawan

- Mensagens : 57
Data de inscrição : 26/05/2016
Idade : 58
Localização : Brasil
 Re: Radiciação !!
Re: Radiciação !!
Solução similar a do poisedom,mas aí vai:
Observe que (y+k)^2=1+(y+k-1)(y+k+1). Logo:
(y+1)=sqrt(1+y(y+2))=sqrt(1+y*sqrt(1+(y+1)(y+3)))=sqrt(1+y*sqrt(1+(y+1)sqrt(1+(y+2)sqrt(…)
Fazendo y=2:
3=sqrt(1+2sqrt(1+3sqrt(1+4sqrt(…)=x -> x+1=4
Solução não é minha.(Um colega a fez)
Observe que (y+k)^2=1+(y+k-1)(y+k+1). Logo:
(y+1)=sqrt(1+y(y+2))=sqrt(1+y*sqrt(1+(y+1)(y+3)))=sqrt(1+y*sqrt(1+(y+1)sqrt(1+(y+2)sqrt(…)
Fazendo y=2:
3=sqrt(1+2sqrt(1+3sqrt(1+4sqrt(…)=x -> x+1=4
Solução não é minha.(Um colega a fez)

John von Neumann jr- Jedi

- Mensagens : 350
Data de inscrição : 18/12/2015
Localização : Brasil
 Re: Radiciação !!
Re: Radiciação !!
Muito boa Poseidom ... obrigado a todos !

glauciomelo- Jedi

- Mensagens : 232
Data de inscrição : 28/02/2016
Idade : 25
Localização : Parnamirin,RN , Brasil
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos