Arcos e ângulos
4 participantes
Página 1 de 1
 Arcos e ângulos
Arcos e ângulos
Sobre arcos e ângulos, assinale o que for correto.
01) O menor ângulo formado pelos ponteiros de um relógio que está marcando 1 hora e 40 minutos é 1700 .
02) Um trem desloca-se na velocidade constante de 60 km/h num trecho circular de raio igual a 500 m. Então, em um minuto ele percorre um arco de 2 rad.
04) Uma pessoa caminhando em volta de uma praça circular descreve um arco de 1600 ao percorrer 120 m. O diâmetro da praça é maior que 100 m.
08) Em 50 minutos, o ponteiro dos minutos de um relógio percorre 5∏/3rad.
Resposta: 01, 02 e 08
01) O menor ângulo formado pelos ponteiros de um relógio que está marcando 1 hora e 40 minutos é 1700 .
02) Um trem desloca-se na velocidade constante de 60 km/h num trecho circular de raio igual a 500 m. Então, em um minuto ele percorre um arco de 2 rad.
04) Uma pessoa caminhando em volta de uma praça circular descreve um arco de 1600 ao percorrer 120 m. O diâmetro da praça é maior que 100 m.
08) Em 50 minutos, o ponteiro dos minutos de um relógio percorre 5∏/3rad.
Resposta: 01, 02 e 08
Camila Satierf- Iniciante
- Mensagens : 27
Data de inscrição : 12/04/2016
Idade : 27
Localização : Uberlândia, MG, Brasil
 Re: Arcos e ângulos
Re: Arcos e ângulos
01) Tendo em vista que, por definição :
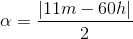
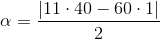
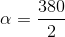
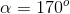
O menor ângulo então é 170º, o que presumo que foi o que você quis dizer. VERDADEIRA
02) 60 km/h = 60/3,6 = 100/6 m/s
Então teremos que:

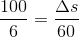
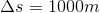
Logo, passaremos para radianos:
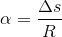
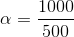
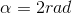
Podemos dizer então que ele percorreu 2rad. VERDADEIRA
04) Por regra de três teremos
160º = 120m
360º = D∏
Então, simplificando e utilizando ∏ ≈ 3,14, teremos que:
Diâmetro ≈ 85
85m < 100m FALSA
08) Se em meia hora o ponteiro dos minutos varre 180º ou ∏
Por regra de três:
pi = 30 minutos
x = 50 minutos
Como resposta, x equivalerá a 5∏/3rad VERDADEIRA
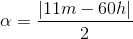
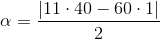
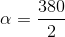
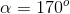
O menor ângulo então é 170º, o que presumo que foi o que você quis dizer. VERDADEIRA
02) 60 km/h = 60/3,6 = 100/6 m/s
Então teremos que:

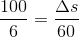
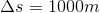
Logo, passaremos para radianos:
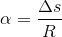
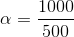
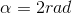
Podemos dizer então que ele percorreu 2rad. VERDADEIRA
04) Por regra de três teremos
160º = 120m
360º = D∏
Então, simplificando e utilizando ∏ ≈ 3,14, teremos que:
Diâmetro ≈ 85
85m < 100m FALSA
08) Se em meia hora o ponteiro dos minutos varre 180º ou ∏
Por regra de três:
pi = 30 minutos
x = 50 minutos
Como resposta, x equivalerá a 5∏/3rad VERDADEIRA

Lukkaz- Padawan

- Mensagens : 84
Data de inscrição : 26/05/2016
Idade : 34
Localização : Niterói, RJ Brasil
 Re: Arcos e ângulos
Re: Arcos e ângulos
Lukkaz
Você aplicou errada a fórmula
α = 380º/2 ---> α = 190º
Este é o MAIOR ângulo. O MENOR ângulo vale 360º - α = 170º
Você aplicou errada a fórmula
α = 380º/2 ---> α = 190º
Este é o MAIOR ângulo. O MENOR ângulo vale 360º - α = 170º

Elcioschin- Grande Mestre

- Mensagens : 73186
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Arcos e ângulos
Re: Arcos e ângulos
Ops, me desculpe, fiquei mais focado em deixar bem organizado do que em fazer as contas, obrigado Elcioschin! Acabei passando direto o 190º e já respondi o 170º subtraído.

Lukkaz- Padawan

- Mensagens : 84
Data de inscrição : 26/05/2016
Idade : 34
Localização : Niterói, RJ Brasil
 Re: Arcos e ângulos
Re: Arcos e ângulos
Tem algumais jeito de resolver a parte 01 sem ser por fórmula?
mari- Estrela Dourada

- Mensagens : 1134
Data de inscrição : 01/09/2015
Idade : 26
Localização : São Paulo
 Re: Arcos e ângulos
Re: Arcos e ângulos
Tem sim
Velocidade do ponteiro dos minutos: Vm = 360º/h = 6º/min
Velocidade do ponteiro das horas: Vh = 360º/12 h = 0,5º/min
Note que Vm = 12.Vh ou Vh = Vm/12
Ângulo entre cada 2 divisões do relógio = 360º/12 = 30º
Exatamente às 13 horas o ponteiro dos minutos está sobre o 12 e ponteiro das horas está sobre o 1; o ângulo entre os ponteiros vale 30º
Após um tempo t o ponteiro dos minutos andou até o 8 (40 min), correspondendo a 8.30 = 240º
No mesmo tempo t o ponteiro das horas andou 240º/12 = 20º
Ângulo entre os ponteiros, contados, no sentido horário, a partir do ponteiro das horas = 240º - 20º - 30º = 190º
Note que este é um ângulo obtuso: o seu replemento vale 360º - 190º = 170º
O menor ângulo (170º) é contado, no sentido anti-horário, a partir do ponteiro das horas
Velocidade do ponteiro dos minutos: Vm = 360º/h = 6º/min
Velocidade do ponteiro das horas: Vh = 360º/12 h = 0,5º/min
Note que Vm = 12.Vh ou Vh = Vm/12
Ângulo entre cada 2 divisões do relógio = 360º/12 = 30º
Exatamente às 13 horas o ponteiro dos minutos está sobre o 12 e ponteiro das horas está sobre o 1; o ângulo entre os ponteiros vale 30º
Após um tempo t o ponteiro dos minutos andou até o 8 (40 min), correspondendo a 8.30 = 240º
No mesmo tempo t o ponteiro das horas andou 240º/12 = 20º
Ângulo entre os ponteiros, contados, no sentido horário, a partir do ponteiro das horas = 240º - 20º - 30º = 190º
Note que este é um ângulo obtuso: o seu replemento vale 360º - 190º = 170º
O menor ângulo (170º) é contado, no sentido anti-horário, a partir do ponteiro das horas

Elcioschin- Grande Mestre

- Mensagens : 73186
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












