Calcule a área do quadrilátero BCMN.

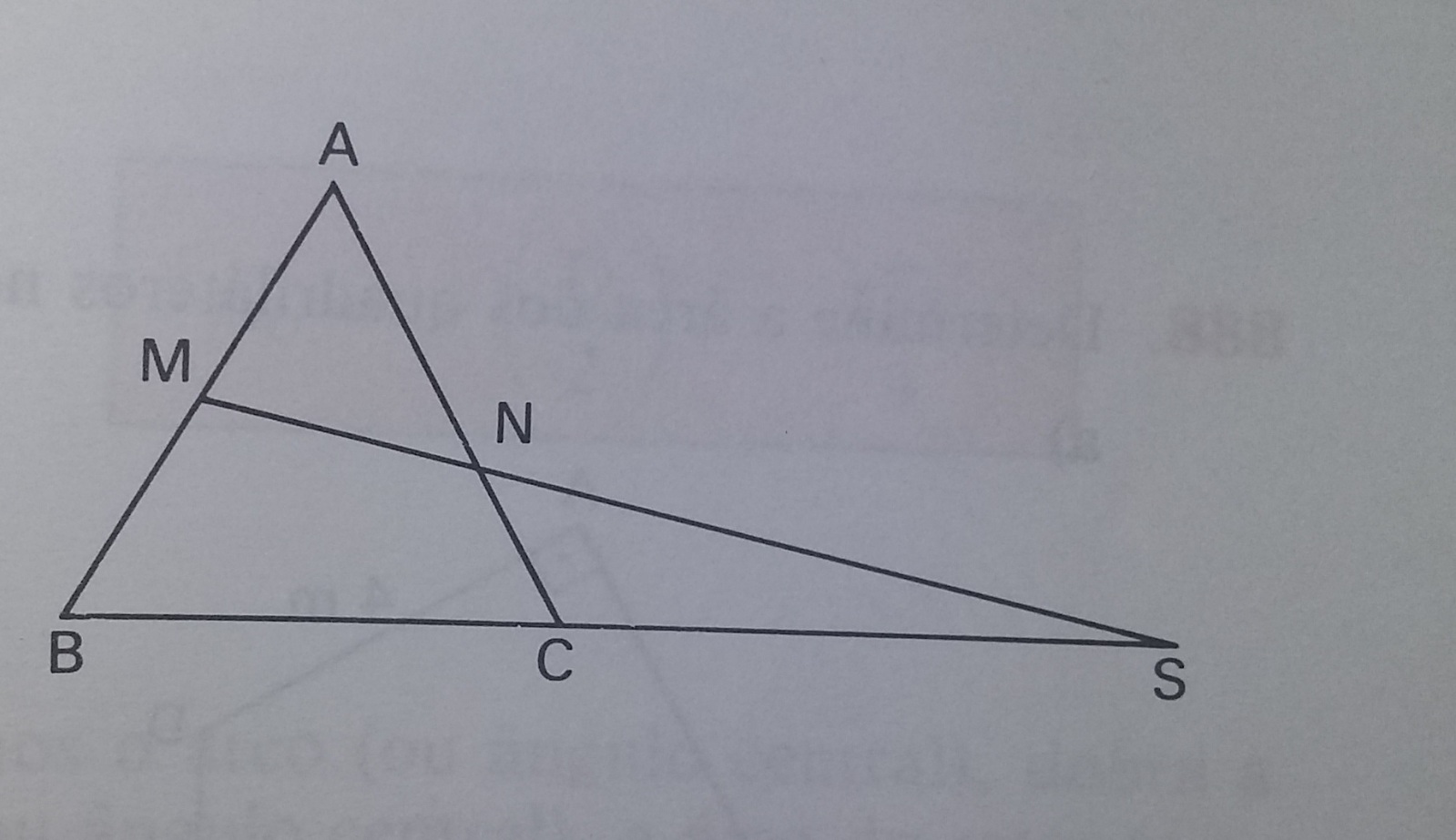
Um triângulo equilátero ABC tem 60 m de perímetro. Prolonga-se a base BC e sobre o prolongamento toma-se CS = 12m. Une-se o ponto S ao meio M do lado AB. Calcule a área do quadrilátero BCMN.

Fazendo as contas:
S(ABC)=L²V3/4=20²V3/4=100V3
S(AMN)/S(ABC)=AM.AN/AB.AC--->S(AMN)/100V3=10.8/20.20--->S(AMN)=100V3*8*10/20 . 20=20V3


S(MBCN)=S(ABC)-S(AMN)=100V3-20V3=80V3

LeoZ,
PF,  siga as regras do fórum. Poste o gabarito . Caso não tenha informe. 

Olá LeoZ.

Penso que encontrei a resolução, porém através de um modo demorado, talvez haja uma resolução mais simples.
Separei por passos para que a resolução não fique tão grande.
O enunciado pede a área do quadrilátero BCNM, correto?
Segue:



Passo 1) Traçar a altura MC

2) MC=10√3 (através de teorema de Pitágoras)

3) Traçar base média MJ=10 ( Metade da base do equilátero)

4) MJ//CS, por teorema de Tales, ∆MJN é semelhante ao ∆NCS

5) Para encontrar a razão de semelhança k,faça : k = MJ/CS=10/12 = 5/6

6)Sabendo que a razão entre áreas de triângulos semelhantes é k² e chamando Area∆MJN=S1 e Area∆NCS=S2 temos:

S1/S2 = (5/6)² => S1/S2=25/36

7) Se Area∆MCN = S3 , podemos montar as relações:

 i)   S3= Area∆MJC-S1
 ii)  S3=Area∆MCS-S2

....Encontrando  as áreas acima com a fórmula que relaciona dois lados e o sen do ângulo compreendido:
 
i) Area∆MJC = (MJ*CJ*senj)/2 = 25√3

ii) Area∆MCS = (CS*MC*sen150º) /2 = 30√3

8)Voltando as relações de 7) :

i)  S3= 25√3- S1 
ii) S3= 30√3 -S2

Se S1/S2=25/36 , podemos afirmar que S1 = 25S2/36

Logo podemos reescrever o sistema da seguinte forma:

S3= 25√3 - 25S2/36 

S3= 30√3 -S2

Resolvendo, encontramos S2=(180√3)/11 e S3= (150√3)/11

9)Area BCNM pedida é dada por : Area∆MCB + S3

50√3 + (150√3)/11 = (700√3)/11

Apesar da resolução,os valores encontrados conferem com os valores do Geogebra.

Espero que tenha entendido, e que esteja correto.Um abraço.
Gustavo.

raimundo, perdoe-me mas, fiquei curioso acerca da sua resolução,pois ficou bastante diferente do que eu pude fazer.

Poderia me explicar como chegou a conclusão que o angulo S=30º ? 
Se B=60º e S=30 , BmC seria 90º.
O seguimento que forma 90º com o lado de um triângulo equilátero e passa pelo ponto médio, não deveria ser somente a altura relativa a esse lado ?


Obrigado. Um grande abraço.

Boa noite!



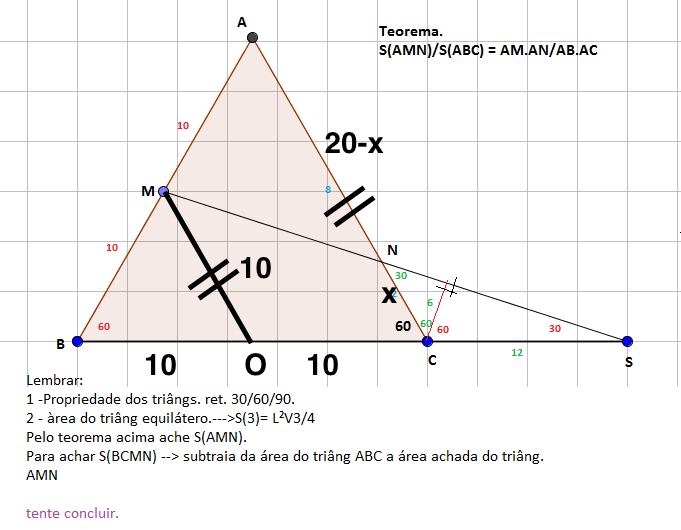
Aproveitando o desenho do Raimundo, nos triângulos SMO e SNC, semelhança:


Agora que temos x podemos calcular a medida de AN, 20-x, e usar o teorema da figura:


Foi essa área que encontrei para o triângulo AMN. Agora, quadrilátero BCNM:


Espero ter ajudado!

Caramba ... duas boas resoluções!!

[1] Lembrando que o teorema, citado pelo Raimundo, sobre a relação entre as áreas é o cálculo delas aproveitando que o ângulo é comum em A.

[2] Se já temos a medida de AN, podemos calcular diretamente a área AMN sem precisar daquela relação.

[3] A menos que se queira usar a relação. Podemos, então, usar uma propriedade das proporções e obter diretamente a área do quadrilátero BCNM.

Gustavo ,
"Manquei feio" . Quando tracei a paralela a AB por C , erradamente concluir a formação de um triângulo retângulo.
"sorry". O Baltuilhe e o Medeiros já colocaram o questão no eixo correto.
Como o probl. se reduz a achar a relação entre AN e NC, deixo mais uma opção para o LeoZ.
Aplicando o teorema de MENELAUS, aplicado no triâng. ABC cortado por MS.

AN/NC.BS/BC.BM/AM=1---->AN/NC.32/12.10/10=1---->AN/NC.8/3=1--->AN/NC=3/8
(AN+NC)/NC=(3+ /3---NC=60/11    

Veja o link , sobre Menelaus. Se ainda persistir dúvidas consulte o livro Vol 2 Geometria Morgado pag.103
https://pir2.forumeiros.com/t83792-semelhanca-de-triangulos

Raimundo, me desculpe por não ter postado o gabarito. Fiquei tanto tempo tentando essa questão sem ter êxito que acabei deixando a ansiedade me levar e esqueci de postar o gabarito.

A resposta do gabarito é realmente (700√3)/11

raimundo pereira escreveu:Gustavo ,
"Manquei feio" . Quando tracei a paralela a AB por C , erradamente concluir a formação de um triângulo retângulo.
"sorry". O Baltuilhe e o Medeiros já colocaram o questão no eixo correto.
Como o probl. se reduz a achar a relação entre AN e NC, deixo mais uma opção para o LeoZ.
Aplicando o teorema de MENELAUS, aplicado no triâng. ABC cortado por MS.

AN/NC.BS/BC.BM/AM=1---->AN/NC.32/12.10/10=1---->AN/NC.8/3=1--->AN/NC=3/8
(AN+NC)/NC=(3+ /3---NC=60/11    

Veja o link , sobre Menelaus. Se ainda persistir dúvidas consulte o livro Vol 2 Geometria Morgado pag.103
https://pir2.forumeiros.com/t83792-semelhanca-de-triangulos

Compreendi Raimundo.Acontece.
As resoluções dos demais amigos realmente foram ótimas.Obrigado pela dica, vou dar uma olhada no teorema. Sempre bom mais uma ferramenta para se usar. Mais uma carta na manga. Ótimo para quem, como eu, visa concursos militares.

Um grande abraço.

Gustavo,
quê "demais amigos"?
Solução tem somente a sua e a do Baltuilhe, e achei ambas muito boas. Eu apenas fiz um comentário sobre o apresentado pelo Raimundo e Baltuilhe.
Abs.