Elipse ITA

por Pedro 01 Dom 21 Fev 2016, 21:51

Seja k > 0 tal que a equação $Elipse ITA Gif$ define uma elipse com distância focal igual a 2. SE (p,q) são as coordenadas de um ponto da elipse, com $Elipse ITA Gif$ , então $Elipse ITA Gif$ é igual a:

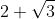
A-) $Elipse ITA Gif$

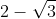
B-) $Elipse ITA Gif$

C-) $Elipse ITA Gif$

D-) $Elipse ITA Gif$

E-) 2

por **gabrieldpb** Dom 21 Fev 2016, 23:00

Como (p,q) pertence a elipse,
(p^2-p)+k(q^2-q)=0 \rightarrow k=\frac{p-p^2}{q^2-q}

Na equação da elipse, vamos completar os quadrados perfeitos:

(x^2-x+\frac{1}{4})+k(y^2-y+\frac{1}{4})=\frac{1}{4}+\frac{k}{4}

(x-\frac{1}{2})^2+k(y-\frac{1}{2})^2=\frac{1}{4}+\frac{k}{4}

\frac{(x-\frac{1}{2})^2}{\frac{1+k}{4}}+\frac{(y-\frac{1}{2})^2}{\frac{1+k}{4k}}=1

Ou seja,

a^2=\frac{1+k}{4} e b^2=\frac{1+k}{4k}

A distância focal é 2c=2, ou sejam c=1

porém, c²=a²-b²

Logo,
\sqrt{\frac{(k-1)(k+1)}{4k}}=1

Condição de existência: k \geqslant 1

k^2-4k-1=0

Logo, respeitando a condição de existência:

k=2+\sqrt{5}

Letra B. Abraço!

Obs.: Eu assumi que a>b, mas poderíamos ter b>a. Nesse caso c²=b²-a², logo:
\sqrt{\frac{(1-k)(k+1)}{4k}}=1

Condição de existência: k \leqslant 1

Logo, -k^2-4k+1=0

Levando em conta condição de existência:
k=\sqrt{5}-2

Abraço!

por Pedro 01 Seg 22 Fev 2016, 18:30

hum legal, eu não tinha pensado em completar os quadrados. Eu só não entendi porque você igualou a 1/4+k/4, não deveria ser 1/4+1/4 ?

por **gabrieldpb** Seg 22 Fev 2016, 19:09

Não, pois ao completar o quadrado de k(y^2-y) eu tenho que colocar o 1/4 dentro do parênteses, mas tem um k multiplicando.Para fazer isso, eu preciso que seja k/4 e assim eu posso fatorar o k e colocar dentro do parênteses.

Abraço!

por Pedro 01 Seg 22 Fev 2016, 23:32

Ahh sim, muito obrigado!!!

por Conteúdo patrocinado

Elipse ITA

Elipse ITA

Re: Elipse ITA

Re: Elipse ITA

Re: Elipse ITA

Re: Elipse ITA

Re: Elipse ITA

Um fórum livre e democrático.