(Escola Naval - 1986) Geometria Espacial
2 participantes
Página 1 de 1
 (Escola Naval - 1986) Geometria Espacial
(Escola Naval - 1986) Geometria Espacial
Sejam  e
e  pontos diametralmente opostos em uma esfera de raio
pontos diametralmente opostos em uma esfera de raio 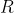 . O volume comum aos cones de revolução inscritos na esfera, com vértices em
. O volume comum aos cones de revolução inscritos na esfera, com vértices em  e em
e em  e cujas alturas são iguais a
e cujas alturas são iguais a 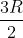 é
é
(A)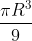
(B)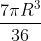
(C)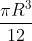
(D)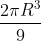
(E)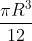
(A)
(B)
(C)
(D)
(E)
Última edição por ALDRIN em Qua 24 Nov 2010, 09:29, editado 1 vez(es)

ALDRIN- Membro de Honra

- Mensagens : 950
Data de inscrição : 29/07/2009
Idade : 41
Localização : Brasília-DF
 Geometria Espacial
Geometria Espacial
Olá,Aldrin.

Primeiro vamos calcular o raio y do cone maior aplicando as relações métricas no triângulo retângulo.
^2=(AF).(FC)\Rightarrow y^2=\frac{R}{2}.\frac{3R}{2}\Rightarrow y^2=\frac{3R^2}{4}\Rightarrow y=\frac{R\sqrt{3}}{2})
Sendo os triângulos CPO e CBF semelhante teremos:
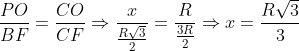
O volume dos dois cones é dado por:
\Rightarrow V=\frac{2\pi R^3}{9})
Falta agora retirar o volume das duas pirâmides de altura igual a R/2.
Como a razão entre volume de sólides semelhantes é igual ao cubo da razão de semelhança teremos:
^3 \Rightarrow k^3=\frac{1}{8})
O volume da pirâmide corresponde a 1/8 do volume do cone de altura R
Logo, o volume comum é dado por:
\Rightarrow V_c=\frac{7\pi R^3}{36})
Alternativa:B

Primeiro vamos calcular o raio y do cone maior aplicando as relações métricas no triângulo retângulo.
Sendo os triângulos CPO e CBF semelhante teremos:
O volume dos dois cones é dado por:
Falta agora retirar o volume das duas pirâmides de altura igual a R/2.
Como a razão entre volume de sólides semelhantes é igual ao cubo da razão de semelhança teremos:
O volume da pirâmide corresponde a 1/8 do volume do cone de altura R
Logo, o volume comum é dado por:
Alternativa:B
adriano tavares- Grande Mestre

- Mensagens : 600
Data de inscrição : 25/07/2009
Localização : São Paulo
 Re: (Escola Naval - 1986) Geometria Espacial
Re: (Escola Naval - 1986) Geometria Espacial
Show de Bola.
Valeu, Doutor Adriano Tavares.
Selva!
Valeu, Doutor Adriano Tavares.
Selva!

ALDRIN- Membro de Honra

- Mensagens : 950
Data de inscrição : 29/07/2009
Idade : 41
Localização : Brasília-DF
 Tópicos semelhantes
Tópicos semelhantes» (Escola Naval) Geometria Espacial
» Escola Naval- Geometria Espacial
» [Escola Naval - 2015 - Geometria Espacial]
» (Escola Naval - 2004) Geometria espacial..
» Geometria Espacial Escola Naval 1987
» Escola Naval- Geometria Espacial
» [Escola Naval - 2015 - Geometria Espacial]
» (Escola Naval - 2004) Geometria espacial..
» Geometria Espacial Escola Naval 1987
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












