Máximo valor da variável

Seja r, s, t, u e v um quinteto de números reais tais que:



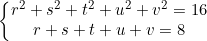
Encontre o maior valor que uma das variáveis pode assumir.

Spoiler:

Problema inspirado neste: https://pir2.forumeiros.com/t39388-valor-minimo-de-e

não consegui encontrar amigo, porém achei outra maneira de achar e=0 no outro problema...kkkk se puder postar a resoluçao agradeço!

Passou-se uma semana, então fica a solução para os interessados:

Spoiler:

Olá colegas;

Eu consegui fazer usando só equações e inequações de 2º grau. Vou deixar essa solução que matutou na minha cabeça que leva ao mesmo resultado do gabarito.
Da primeira equação do sistema surge que se existem soluções a,b,c,d,e , então vale a relação de equivalência:

(I)[latex] \text{ }a + b + c + d + e =8 \Leftrightarrow \forall k, k \in \mathbb{R}, \text{ } k \neq 0\text{ } \text{ } (a + b + c + d + e)k = 8k [/latex]

(II) [latex]a + b + c + d + e =8[/latex]

(III)[latex]a^2 + b^2 + c^2 + d^2 + e ^2 = 16[/latex]

[latex](I), (III) \implies (a^2 + b^2 + c^2 + d^2 + e ^2) + (a + b + c + d + e)k = (16) + (8k) \implies [/latex]

[latex] a(a+k) + b(b+k) + c(c+k) + d(d+k) + e(e+k) = 16 + 8k [/latex]

Moral da história, se existe uma solução a,b,c,d,e para equações (II) e (III) mutualmente, então, para qualquer k real não nulo, ela também é para solução da equação:

(IV)[latex](a^2 + b^2 + c^2 + d^2 + e ^2) + (a + b + c + d + e)k = 16 + 8k[/latex]

(V) Seja f(x) = x(x+k) note que f(x) possui mínimo e é tal que [latex]f(x) \ge -\frac{k^2}{4}[/latex]

[latex](III) \implies a(a+k) + b(b+k) + c(c+k) + d(d+k) + {[e(e+k)]} = 16 + 8k \implies [/latex]

(VI)[latex]f(a) + f(b) + f(c) + f(d) = 16 + 8k - {[e(e+k)]}[/latex]

[latex](V) \implies f(a) \ge -\frac{k^2}{4}, \text{ }\text{ } f(b) \ge -\frac{k^2}{4}, \text{ }\text{ } f(c) \ge -\frac{k^2}{4}, \text{ }\text{ } f(d) \ge -\frac{k^2}{4} \implies[/latex]

(VII)[latex]f(a) + f(b) + f(c) + f(d) \ge -k^2[/latex]

[latex](VI), (VII) \implies 16 + 8k - {[e(e+k)]} \ge -k^2 \implies 0 \ge e(e+k) -(k^2 +8k +16) [/latex]

(VIII)[latex]\text{ }-k^2 + (e-8)k - (e^2-16) \le 0[/latex]

Segunda moral da história, se existe um valor de "e" que satisfaça (II) e (III), então para qualquer k real não nulo a inequação acima é verdadeira.
Note que, para qualquer k ser sempre solução na inequação acima, o discriminante na variável "k" deve ser menor ou igual a zero:

(VIII) [latex]({e-8})^2 +4(e^2 -16) \le 0 \implies e(e-\frac{16}{5})\le 0 \implies 0 \le e \le \frac{16}{5}[/latex]

Em todo caso, essa questão é meio problemática porque você ainda teria que mostrar que existe uma solução na qual [latex]e = \frac{16}{5}[/latex], já que ele pede o maior valor que as variáveis podem assumir. Nem na minha e nem na resposta do colega anterior esse fato é validado (não consegui). Agora, se essa não for de fato a intenção do enunciado(obter o valor máximo), você poderia escolher uma cota superior mais simples de obter:

[latex]a^2 + b^2 + c^2 + d^2 = 16 -e^2 ,\text{ }\text{ } a^2 + b^2 + c^2 + d^2 \ge 0 \implies

16 -e^2 \ge 0 \implies -4 \le e \le 4 [/latex]

Essa discussão vem da diferença entre os termos matemáticos 'máximo' e 'cota superior'.

Bons estudos