[Resolvido](ITA) Conjunto das raízes das equações

Considere as equações 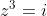e onde . Seja S1 o conjunto das raízes da primeira equação e S2 o da segunda. Então:


a)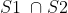 é vazio.
b)
c) S1 possui apenas dois elementos distintos.
d)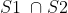 é unitário.
e)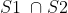 possui 2 elementos.

z³ = i ----> z³ = cos(pi/2) + i*sen(pi/2) ----> z = [cos(pi/2) + i*sen(pi/2)]^(1/3)

z = cos[(2kpi + pi/2)/3 + i*sen[(2kpi + pi/2)/3]

Para k = 0 ----> z1 = cos(pi/6) + i*sen(pi/6) ----> z1 = V3/2 + i/2

Para k = 1 ----> z2 = cos(5pi/6) + i*sen(5pi/6) ----> z2 = - V3/2 + i/2

Para k = 2 ----> z3 = cos(3pi/2) + i*sen(3pi/2) ----> z3 = - i


Substituindo cada uma das 3 raízes na expressão z² + (2 + i)*z + 2i nota-se que, para nenhuma das 3 raízes chega-se no valor zero.

Logo ----> S1 inter S2 é vazio ----> Alternativa A

Certo! Acho que era a minha apostila que devia estar com o gabarito errado
Acabei de dar uma conferida, e diz que a alternativa d) é a correta.
mas tentei fazer e não encontrei nenhuma raiz semelhante entre os conjuntos também

Obrigada!

Esta resolução está errada, o gabarito está certo!
Uma das raízes da 1ª equação é = -i
E uma das raízes da segunda tbm eh = -i
Logo a intersecção dos dois é um conjunto unitário.
Vendo por soma e produto na segunda é fácil perceber que as raízes são -i e
-2. De vez em quando procuro uns exercício aqui pra treinar, acabei vendo que estava errado.

z³ = i ----> z³ = cos(pi/2) + i*sen(pi/2) ----> z = [cos(pi/2) + i*sen(pi/2)]^(1/3) 

z = cos[(2kpi + pi/2)/3 + i*sen[(2kpi + pi/2)/3]

Para k = 0 ----> z1 = cos(pi/6) + i*sen(pi/6) ----> z1 = V3/2 + i/2

Para k = 1 ----> z2 = cos(5pi/6) + i*sen(5pi/6) ----> z2 = - V3/2 + i/2

Para k = 2 ----> z3 = cos(3pi/2) + i*sen(3pi/2) ----> z3 = - i


A duas maneiras agora:

(I) Substituindo na outra equação, percebe-se que somente "-i" é raiz.
................. (-i)²+(2+i)(-i)+2i = i²-2i-i²+2i = 0

ou

(I) Resolvendo a outra equação: z²+(2+i)z+2i
.. ∆ = 3-4i

z=[-(2+i)±  √(3-4i)]/2

mas, √(3-4i)=a+bi ............ 3-4i=a²+2abi-b² .................... a²-b²=3 e ab=-2 .............. a=2 e b=-1 ou a=-2 e b=1, não faz diferença! 

z1=[-2-i+(2-i)]/2=-i
z2=[-2-i-(2-i)]/2=-2


Portanto, S1∩S2 é unitário.