[Escola Naval - 2015 - Conjuntos com trigono]

por RamonLucas Dom 06 Set 2015, 19:42

(Concurso de Admissão à Escola naval / CPAEN-2015. Prova: Amarela. Questão 13)

As curvas representantes dos gráficos de duas funções de variável real y=f(x) e y=g(x) interceptam-se em um ponto P_o(x_o,y_o), sendo $x_{o}\epsilon D(f)\cap D(g)$ É possível definir o ângulo formado por essas duas curvas no ponto P_ocomo sendo o menor ângulo formado pelas retas tangentes àquelas curvas no ponto P_o. Se f(x)=x²-1,g(x)=1-x² e θ é o ângulo entre as curvas na interseção de abscissa positiva, então, pode-se dizer que o valor da expressão $\begin{bmatrix} (\sqrt{6}-\sqrt{2})sen\left ( \frac{5\pi }{12} \right )+cos2\Theta -cossec\left ( \frac{7\pi }{6} \right ) \end{bmatrix}^{\frac{1}{2}}$

(A) $\frac{\sqrt{82}}{5}$

(B) $3\frac{\sqrt{2}}{5}$

(C) $\frac{68}{25}$

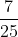
(D) $\frac{7}{25}$

(E) $2\frac{\sqrt{}17}{5}$

por **Elcioschin** Dom 06 Set 2015, 21:33

As duas curvas se cortam em (1, 0) --> abcissa positiva

y = x² - 1 ---> y' = 2x ---> y'(-1) = 2.1 ---> y'(1) = 2 ---> tgα = 2
y = 1 - x² ---> y' = -2x ---> y'(-1) = -2.1 ---> y'(1) = -2 ---> tgβ = -2

θ = β - α ---> tgθ = tg(β - α) ---> tgθ = (tgβ - tgα)/(1 + tgβ.tg α) --->

tgθ = (- 2 - 2)/[1 + (-2).2] ---> tgθ = 4/3 ---> cosθ = 4/5 ---> senθ = 3/5

(√6 - √2).sen(5pi/12) = (√6 - √2).sen75º = (√6 - √2).(√6 + √2)/4 = 1

cos(2.θ) = 2.cos²θ - 1 = 2.(3/5)² - 1 = - 7/25

- csc(7.pi/6) = -1/sen(210) = - 1/(-1/2) = 2

E² = 1 - 7/25 + 2 ---> E² = 68/25 ---> E² = 4.17/25 ---> E = 2.√17/5

por vieirasouza Dom 29 maio 2016, 15:31

poderia dar um embasamento em sua resolução?

por **Medeiros** Dom 29 maio 2016, 17:27

vieirasouza escreveu:poderia dar um embasamento em sua resolução?

[Escola Naval - 2015 - Conjuntos com trigono] 1zzjck7

Élcio
você está resolvendo sem base nos princípios matemáticos? Você não poderia demonstrar cada princípio e propriedade usada na resolução? he he he

por **Elcioschin** Dom 29 maio 2016, 20:52

Vou dar o embasamento para o colega:

1) Você precisa saber derivadas básicas
2) Você precisa fazer um esboço das duas curvas e do ponto dado, num sistema xOy e desenhar as duas tangentes, no ponto dado.
3) Você precisa saber que numa reta y = a.x + b o valor a, é o coeficiente angular da reta (tangente que ela faz com o eixo x
4) Você precisa saber que tg(m - n) = (tgm - tgn)/(1 - tgm.tgn)
5) Você precisa saber calcular o seno e o cosseno de um ângulo, conhecendo a tangente dele
6) E, finalmente você precisa ser hábil ao fazer as contas exigidas.