Expansão
2 participantes
PiR2 :: Física :: Termologia
Página 1 de 1
 Expansão
Expansão
Um recipiente cilíndrico de seção uniforme e
termicamente indilatável é provido de um êmbolo que
pode deslizar em seu interior com atrito desprezível.
O recipiente contém 5 moles de um gás ideal a 27°C,
estando o êmbolo a 10 cm da base. Aquece-se o gás muito
lentamente (de modo que a pressão permaneça constante
durante o processo) até que o êmbolo suba 1 cm, como
ilustra a figura.

Considere a constante universal dos gases ideais
R = 2 cal/mol.K. O trabalho realizado pelo gás durante a
expansão foi
(A) 300 cal
(B) 250 cal
(C) 200 cal
(D) 150 cal
(E) 100 cal
Gabarito A
termicamente indilatável é provido de um êmbolo que
pode deslizar em seu interior com atrito desprezível.
O recipiente contém 5 moles de um gás ideal a 27°C,
estando o êmbolo a 10 cm da base. Aquece-se o gás muito
lentamente (de modo que a pressão permaneça constante
durante o processo) até que o êmbolo suba 1 cm, como
ilustra a figura.

Considere a constante universal dos gases ideais
R = 2 cal/mol.K. O trabalho realizado pelo gás durante a
expansão foi
(A) 300 cal
(B) 250 cal
(C) 200 cal
(D) 150 cal
(E) 100 cal
Gabarito A
awake188- Padawan

- Mensagens : 83
Data de inscrição : 21/03/2015
Idade : 31
Localização : Salvador
 Re: Expansão
Re: Expansão
Observe que a pressão é mantida constante, logo a Lei de Charles é aplicável a esta situação. Enunciando a lei:
"Quando a pressão em uma amostra de gás é mantida constante, a temperatura (Kelvins) e o volume estarão diretamente relacionados."
Isto significa que há uma relação de proporção entre o volume e a temperatura, de modo que sua razão se mantém constante ao longo de todo o processo de expansão:
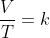


Qualquer volume de um sólido é dado pelo produto entre a área da base e sua altura. No caso de um cilindro uniforme temos que V = pi.r²h. Contudo, o problema não nos fornece o raio da base e nem uma maneira de calculá-lo, portanto irei assumir apenas que existe uma área A desconhecida. A altura inicial e final certamente são 10 cm e 11 cm, respectivamente.

Como não ocorre mudança da área da base do cilindro, A e A0 são iguais. A temperatura final durante a expansão equivale a:
&space;\to&space;T&space;=&space;330&space;K)
O trabalho realizado a uma pressão constante será:
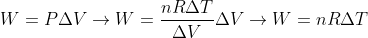
Agora basta substituir com os dados fornecidos:
&space;K)

"Quando a pressão em uma amostra de gás é mantida constante, a temperatura (Kelvins) e o volume estarão diretamente relacionados."
Isto significa que há uma relação de proporção entre o volume e a temperatura, de modo que sua razão se mantém constante ao longo de todo o processo de expansão:
Qualquer volume de um sólido é dado pelo produto entre a área da base e sua altura. No caso de um cilindro uniforme temos que V = pi.r²h. Contudo, o problema não nos fornece o raio da base e nem uma maneira de calculá-lo, portanto irei assumir apenas que existe uma área A desconhecida. A altura inicial e final certamente são 10 cm e 11 cm, respectivamente.
Como não ocorre mudança da área da base do cilindro, A e A0 são iguais. A temperatura final durante a expansão equivale a:
O trabalho realizado a uma pressão constante será:
Agora basta substituir com os dados fornecidos:

MCarsten- Recebeu o sabre de luz

- Mensagens : 150
Data de inscrição : 25/01/2013
Idade : 28
Localização : Lages - SC
 Re: Expansão
Re: Expansão
MCarsten escreveu:Observe que a pressão é mantida constante, logo a Lei de Charles é aplicável a esta situação. Enunciando a lei:
"Quando a pressão em uma amostra de gás é mantida constante, a temperatura (Kelvins) e o volume estarão diretamente relacionados."
Isto significa que há uma relação de proporção entre o volume e a temperatura, de modo que sua razão se mantém constante ao longo de todo o processo de expansão:
Qualquer volume de um sólido é dado pelo produto entre a área da base e sua altura. No caso de um cilindro uniforme temos que V = pi.r²h. Contudo, o problema não nos fornece o raio da base e nem uma maneira de calculá-lo, portanto irei assumir apenas que existe uma área A desconhecida. A altura inicial e final certamente são 10 cm e 11 cm, respectivamente.
Como não ocorre mudança da área da base do cilindro, A e A0 são iguais. A temperatura final durante a expansão equivale a:
O trabalho realizado a uma pressão constante será:
Agora basta substituir com os dados fornecidos:
Entendi, cara. Muito obrigado e bela explicação! Eu achei a temperatura final normalmente, mas pensei que o trabalho seria a variação da energia interna do gás (U=3/2nRT), ai só dava 450 cal.
awake188- Padawan

- Mensagens : 83
Data de inscrição : 21/03/2015
Idade : 31
Localização : Salvador
 Re: Expansão
Re: Expansão
Lembre-se que a variação energia interna não equivale somente ao trabalho realizado durante o processo, mas também à adição do calor fornecido ao sistema, a não ser que se trate de um processo adiabático, o que não é o caso, em que então se teria uma variação de energia interna igual ao trabalho realizado sobre o sistema.
Vejamos a relação entre o trabalho e a variação da energia interna a partir da equação de Clapeyron para os gases ideais:
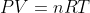
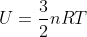
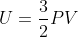
Se considerarmos que V seja a variação do volume durante a expansão:
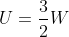
Substituindo W por 300 cal, obtemos:
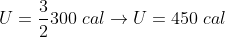
Que é o resultado que você obteve, comprovando o que comentei acima.
Vejamos a relação entre o trabalho e a variação da energia interna a partir da equação de Clapeyron para os gases ideais:
Se considerarmos que V seja a variação do volume durante a expansão:
Substituindo W por 300 cal, obtemos:
Que é o resultado que você obteve, comprovando o que comentei acima.

MCarsten- Recebeu o sabre de luz

- Mensagens : 150
Data de inscrição : 25/01/2013
Idade : 28
Localização : Lages - SC
PiR2 :: Física :: Termologia
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












