Complexos

por victorguerra03 Qui 30 Abr 2015, 19:00

Resolvendo a equação Complexos LpcfwwDdC9+sWc4oEQA7

no conjunto dos números complexos, conclui-se sobre as suas soluções que:

a) Nenhuma delas é um número inteiro.
b) A soma delas é Complexos ALIJCACADs=

.
c) Estas são em número de Complexos ALIJCACADs=

e são distintas.
d) Estas são em número de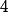 $Complexos Mathtex$ e são Complexos ALIJCACADs=

a

distintas.
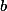e) Uma delas é da forma $Complexos Mathtex$ com $Complexos Mathtex$ real não nulo.

Nota: por $Complexos Mathtex$ denotamos o conjugado do número complexo $Complexos Mathtex$ .
Gab: C

Igualei a² - b² = 2 + a
2abi = -bi

Encontrei a = -1/2 e b² = -5/4, porém não sei pq o gabarito é letra c. Grato desde já.

por **Elcioschin** Qui 30 Abr 2015, 19:28

Fazendo z = a + bi

...... ______....................... _________
z² = (2 + z) ---> (a + bi)² = (2 + a + bi) ---> a² - b² + 2abi = (2 + a) - bi

1) 2ab = - b ---> 2ab + b = 0 ---> b.(2a + 1) = 0 ---> Temos duas possibilidades:

1.1 ---> b = 0 ---> a² - b² = 2 + a ---> a² - a - 2 = 0 ---> Raízes a = - 1 e a = 2

Soluções ---> z = -1 e z = 2

1.2 ---> 2a + 1 = 0 ---> a = - 1/2 ---> (-1/2)² + b² = 2 - 1/2 ---> b = - 5/4 ou b = 5/4

Soluções---> z = -1/2 - (5/4).i e z = - 1/2 + (5/4).i

Complexos

Complexos

Re: Complexos

Um fórum livre e democrático.