Número Primo

por JonasDSS Qua 29 Abr 2015, 12:33

Se p é um número primo e as duas raízes da equação x²+px-444p=0 são números inteiros, então:

A.( )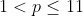 $Número Primo Gif$

B.( )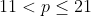 $Número Primo Gif$

C.( )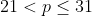 $Número Primo Gif$

D.( )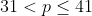 $Núme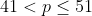ro Primo Gif$

E.( ) $Número Primo Gif$

por **Elcioschin** Qua 29 Abr 2015, 13:52

x² + px - 444.p = 0

∆ = b² - 4ac ---> ∆ = p² - 4.1.(-444.p) ---> ∆ = p² + 1776.p

Devemos ter ∆ = k² --> onde k é inteiro ---> p² + 1776.p = k² ---> k² - p² = 1776 --->

(k - p).(k + p) = 2⁴.3.37 ---> Pares de divisores positivos de 1776 --->

(1, 1776), (2, 888), (3, 592), (4, 444), (6, 296), (8, 222), (12, 148), (16, 111), (24, 74), (48, 37)

Podemos montar o sistema de equações, para o par (x, y):

k - p = x
k + p = y

Somando ambas --> 2k = x + y ---> x + y deve ser par.
Ou são ambos pares ou ambos ímpares

Os pares (1, 1776), (3, 592) e (48, 37) não servem

O único par que atende é (24, 74)

k - p = 24
k + p = 74

2k = 98 ---> k = 49 ---> p = 25 ---> Alternativa C

por **Carlos Adir** Qua 29 Abr 2015, 14:17

Mestre Elcio, está correto?
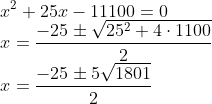
$\\ x^2+25x-11100=0 \\ x = \dfrac{-25 \pm \sqrt{25^2+4 \cdot 1100}}{2} \\ x = \dfrac{-25 \pm 5\sqrt{1801}}{2}$
fora que 25 não é primo '-'

Mestre Elcio, tenho outra resolução:
$\\ x^2+px-444p=0 \\ x = \dfrac{-p\pm \sqrt{p^2-4 \cdot 1 \cdot (-444p)}}{2} \\ x=\dfrac{-p \pm \sqrt{p(p+1776)}}{2}$
Para o valor dentro da raiz ser um quadrado perfeito, é necessário que a soma de p+1776 dê um quadrado como 4,9, 16 multiplicado por p.
Isto é, queremos que dê p(p . k²)
$\\ x=\dfrac{-p \pm \sqrt{p(p \cdot k^2)}}{2} \\ x = p \left(\dfrac{-1 \pm k}{2} \right )$
Agora, é necessário que:
$p+1776=k^2p \Rightarrow p\left(k^2-1 \right ) = 1776=2^{4}\cdot 3 \cdot 37$
Podemos testar alguns valores para k. Devemos testar os impares, pois como visto acima, subtrairemos -1 ±k deve ser multiplo de 2, e isso ocorre de k for impar.
$\begin{cases}k=3 \\ k=5 \\ k=7 \end{cases}\Rightarrow \begin{cases}p\left(3^2-1 \right ) =2^{4}\cdot 3 \cdot 37 \\ p\left(5^2-1 \right )=2^{4}\cdot 3 \cdot 37 \\ p(7^2-1)=2^{4} \cdot 3 \cdot 37\end{cases} \Rightarrow \begin{cases}p=222 \\ p=74 \\ p=37 \end{cases}$
O primeiro nem o segundo é primo, então, temos que p=37.

Ou seja, D)

Vamos verificar:
$\\ x^2+37x-16428=0 \\ x = \dfrac{-37 \pm \sqrt{37^2 - 4 \cdot (1) \cdot (-16428)}}{2} \\ x = \dfrac{-37 \pm 259}{2}$

P=37 realmente dá certo.

por **Elcioschin** Qua 29 Abr 2015, 14:37

Carlos Adir

Você tem toda a razão meu caro (eu esqueci de checar que p = 25 não era primo).

Verifiquei minha solução e descobri o meu erro: eu só coloquei os divisores positivos de x, quando deveria também colocar também os negativos. E isto é plenamente confirmado na sua solução, onde uma raiz é positiva e a outra negativa.

Obrigado pelo alerta

por **Ashitaka** Qua 29 Abr 2015, 14:43

Acho mais fácil, ali no fim, Carlos, testar os valores de p em vez de k.
p só pode ser 1, 2, 3 ou 37. Testando esses valores de p, temos certeza que vimos todos os casos possíveis.

por **Ashitaka** Qua 29 Abr 2015, 14:44

Elcioschin escreveu:x² + px - 444.p = 0

∆ = b² - 4ac ---> ∆ = p² - 4.1.(-444.p) ---> ∆ = p² + 1776.p

Devemos ter ∆ = k² --> onde k é inteiro ---> p² + 1776.p = k² ---> k² - p² = 1776 --->

(k - p).(k + p) = 2⁴.3.37 ---> Pares de divisores positivos de 1776 --->

(1, 1776), (2, 888), (3, 592), (4, 444), (6, 296), (8, 222), (12, 148), (16, 111), (24, 74), (48, 37)

Podemos montar o sistema de equações, para o par (x, y):

k - p = x
k + p = y

Somando ambas --> 2k = x + y ---> x + y deve ser par.
Ou são ambos pares ou ambos ímpares

Os pares (1, 1776), (3, 592) e (48, 37) não servem

O único par que atende é (24, 74)

k - p = 24
k + p = 74

2k = 98 ---> k = 49 ---> p = 25 ---> Alternativa C

Elcioschin, acredito que o erro nasce na parte em destaque, onde faltou p.

por **Carlos Adir** Qua 29 Abr 2015, 14:48

Sim, pensei em colocar isso no final.
Mas era bastante óbvio que p=37, porque se p=2 ou p=3, teriamos que:
p . (k²-1) = p (k-1)(k+1)
O valor de k+1 seria 37 e então faria k-1 = 35, multiplo de 7, daria errado.
O valor de k-1 seria 37 e então k+1 = 39, outro primo, daria errado.
Assim, a unica solução seria p=37.