Seno e Cosseno na resolução de equação

Se (x+5)²+(y-12)²=14², determine o valor mínimo de x²+y².

Resolução:
fazendo x+5=14 cos a
e y-12=14 sen a, temos:
x²+y²= (14 cos a-5)²+(14sen a+12)²=365+28(12sen a- 5 cos a)
então o valor mínimo assumido por 12sena-5cosa segue a equação

no caso de 12=a e -5=b
tem-se -13 como valor mínimo
substituindo -13 no lugar de 12sen a-5cos a
x²+y²=365+28.(-13)=1

Poderiam me explicar o porquê desses senos e cosseno tão aleatórios?
Se tiverem outra resolução, enviem por favor.
grato desde já.

Pensa em geometria analítica: 
(x+5)²+(y-12)²=14²
É uma equação de uma circunferencia de centro C(-5,12) e raio 14.

Como você quer o mínimo de x²+y², é legal pensar na distância de um ponto (x,y) a origem O(0,0); 

distancia = \sqrt{x^2+y^2}
distancia^2= x^2+y^2

Então o objetivo é encontrar a menor distância da origem até um ponto da circunferência:

Faça um desenho e perceba que esse tamanho é 
|dist(C,O) - R|=|\sqrt{12^2+5^2}-14|=|13-14|=1

O mínimo de x^2+y^2 é  1^2 =1

Ah, e os senos e cossenos não são aleatórios...
Concorda que é ruim ter duas incógnitas?

Aí como é uma soma de quadrados igual a constante, você lembra da relação trigonométrica fundamental:

sen^2(x)+cos^2(x)=1

Aí : 
x+5=14 cos(a)
e
y-12=14 sen(a)

Você fica com uma equação que é verdadeira pela relação fundamental. 

Pra achar o mínimo de 12sen(a)- 5 cos (a)
você divide e multiplica a equação por \sqrt{12^2+5^2}=13
E fica com: 
13(\dfrac{12}{13}sen(a)-\dfrac{5}{13}cos(a))
Usa que cos(\alpha)= \dfrac{12}{13}
e
sen(\alpha)=\dfrac{5}{13}

Com isso, você tem:
13(cos(\alpha)sen(a)-sen(\alpha)cos(a))
13(sen(\alpha-a))
Que tem -13 como seu valor mínimo... Aí continua a substituição lá do que você postou que voce realmente acha 1. 


(Essa ideia de sen e cos é muito usada em problemas para parametrizar circunferencias e elipses em geometria analítica. É legal saber substituir quando vale a pena)

Muito obrigado. Entendi tudo. Agora só preciso aprender quando usar, ou seja, o mais difícil. (E só agora percebi que é uma equação de circunferência)

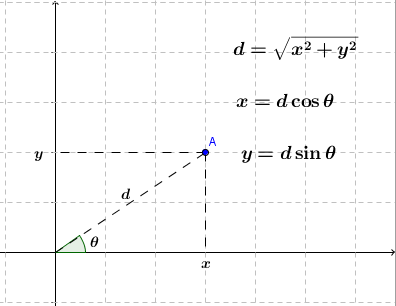
Para qualquer ponto no plano:

Sabe que eu tenho um conhecimento relativamente bom em trigonometria, mas nunca pensei em usar seno e cosseno no plano cartesiano. Obrigado aos dois. abriram minha mente.

E antes que eu me esqueça, Euclides, como é que você elabora os gráficos?

Software: Geogebra, gratuito.

Download: https://www.geogebra.org/

Está certo. Obrigado novamente, hehe.

camillantunes, excelente resolução por Geometria Analitica. Bem legal =)

Pessoal, uma duvida. Quando faz-se x+5=14 cos(a) , isso nao limita os valores de "x" ,não? Quero dizer, -14 < x+5 < 14