Base vetorial

por nandofab Sex 23 Jan 2015, 15:24

Mostre que 2 vetores não paralelos no R² sempre formam uma base vetorial no R²

por **Carlos Adir** Sex 23 Jan 2015, 15:58

Sejam os vetores v=(a, b) e u=(c, d), pela hipótese, podemos então escrever qualquer ponto em função dos vetores, isto é, (x,y)=(am + nc , bm + dn)
E realmente podemos, temos então:
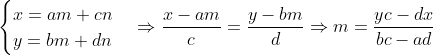
$\begin{cases}x=am+cn \\ y=bm+dn \end{cases} \Rightarrow \dfrac{x-am}{c}=\dfrac{y-bm}{d} \Rightarrow m=\dfrac{yc-dx}{bc-ad}$
Ou
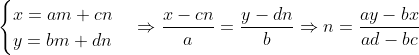
$\begin{cases}x=am+cn \\ y=bm+dn \end{cases} \Rightarrow \dfrac{x-cn}{a}=\dfrac{y-dn}{b} \Rightarrow n=\dfrac{ay-bx}{ad-bc}$
E o porquê de dois vetores não serem paralelos, isto é, tem-se que se dois vetores forem paralelos, então podemos escrever um em função do outro.
v=u.k --> (a, b) = (c, d) . k --> a=ck; b=dk
Então, substituindo na relação achada:
$\\ m=\dfrac{yc-dx}{(dk)c-(ck)d}=\dfrac{yc-dx}{0}; \\ n=\dfrac{ay-bx}{(ck)d-(dk)c}=\dfrac{ay-bx}{0}$
Ou seja, uma indeterminação.

Um exemplo é o segunte, dados os vetores (1,2) e (3, -1), descubra a equação que dê o ponto (5, 0)
Por sistema:
$\\ \begin{cases}5=1m+3n \\ 0=2m+(-1)n \end{cases}\\ n=2m \\ m=\dfrac{5}{7} \Rightarrow n = \dfrac{10}{7} \\ \left(5,0 \right )=\dfrac{5}{7} \left(1,2 \right )+\dfrac{10}{7}\left(3,-1 \right )$

por nandofab Seg 26 Jan 2015, 14:40

Perfeito. Obrigado!!

por Conteúdo patrocinado

Base vetorial

Base vetorial

Re: Base vetorial

Re: Base vetorial

Re: Base vetorial

Um fórum livre e democrático.