máximo e mínimo

por **Maria das Graças Duarte** Sex 23 Jan 2015, 00:04

1. O lucro mensal de uma empresa é dado por L = -x²+30x-5, onde x é a quantidade mensal vendida.

a) Qual o lucro mensal máximo possível?

b) Entre que valores deve variar x para que o lucro mensal seja no mínimo igual a 195?

por lukeoluk Sex 23 Jan 2015, 00:18

Bom, para começar a resolução do problema, é necessário perceber que a parábola do lucro possui concavidade para baixo, ou seja, possui máximo e não possui um mínimo. Dito isso, é necessário apenas achar o X do vértice e substituir na equação para a resolução da questão a. -30/-2=15 > -225 + 225.2+ 5= 230

Para a questão b, deve-se colocar o valor L como 195 e resolver normalmente pelas equações de Girard (soma e produto)
-x² + 30x - 200=0 o que por Girard nos dará as raízes 10 e 20 ou seja 10≤x≤20

por **Maria das Graças Duarte** Sex 23 Jan 2015, 00:37

-225 + 225.2+ 5= 230
não entendi essa substituição

por lukeoluk Sex 23 Jan 2015, 00:43

De fato, fiz errado, eu troquei o sinal do 5 na hora de fazer as contas, o valor real é 220, me desculpe, a conta ficaria -x² + 30x - 5 em que x=15 > -15² + 30.15 - 5 > -225 + 225.2 - 5 > 220

por **Euclides** Sex 23 Jan 2015, 00:56

Maria das Graças,

a parábola da figura abaixo é o gráfico da função lucro.

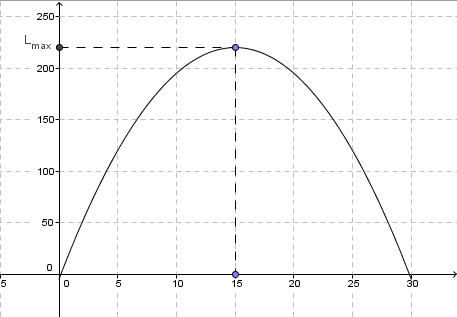
máximo e mínimo Aten_o

o ponto máximo dessa curva ocorre para x igual ao ponto médio entre as raízes. Esse ponto pode ser obtido pelo cálculo

x_{m}=-\frac{b}{2a} \;\;\;\;\text{sendo} \;\;\;a=-1,\;\;\;b=30\;\;\;\;\to\;\;\;\;x_m=-\frac{30}{-2}\;\;\to\;\;x_m=15

para encontrar o valor correspondente ao lucro, devemos substituir esse número por x na equação da parábola:

L=-(15)^2+30(15)-5\;\;\to\;\;L=220

PS: o assunto é álgebra (estudo das funções) para onde vou mover a questão.

por **Maria das Graças Duarte** Sex 23 Jan 2015, 01:02

mestre fala em que valores deve variar

por **Carlos Adir** Sex 23 Jan 2015, 01:33

Você pode também achar pelo seguinte:
-x²+30x-5

Aqui usamos algo chamado de completar quadrados:

-x²+2 . 15 x - 5

-x²+2 . 15 x - 15² + 220

-(x²-2.15x+15²)+220

-(x-15)²+220

Então, o máximo será 220, e será o ponto -(-15) = 15

Caso entenda melhor desta maneira, também funciona.

por **Medeiros** Sex 23 Jan 2015, 04:41

Maria das Graças,
aproveitando o desenho do Euclides para responder ao item b, podemos usar o artifício de mudar o eixo dos x de tal forma que cruze o eixo y exatamente no ponto 195 pedido -- e obtendo uma nova f(x). Desta forma, o intervalo pedido ficará entre as raízes da nova f(x).

Note que a nova f(x) foi "rebaixada" é temos:
L = -x^2 + 30x - 5
L' = -x^2 + 30x - 5 - 195 --------> L' = -x^2 + 30x - 200

máximo e mínimo 2qiso75