Maximos e Minimos

(Lei de refração de Snellius) Considere uma reta "s" e dois pontos P e Q localizados em semiplanos opostos de acordo a figura. Uma particula vai de P a M com velocidade constante "u" e movimento retilineo, em seguida, vai de M a Q com velocidade constante "v", tambem em movimento retilineo. Mostre que o tempo do percurso será minimo se

sen(α)/u = sen(β)/v



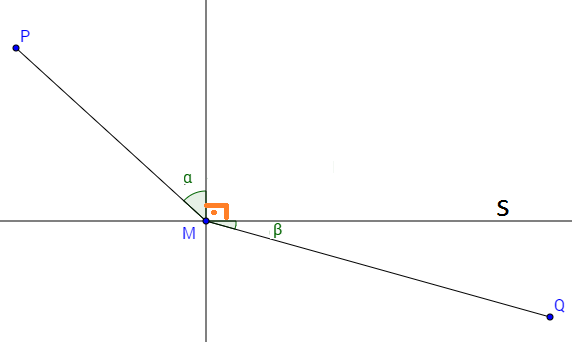
Pessoal, acabei esquecendo de colocar mas a reta "s" é o eixo Ox

O ângulo β da sua figura deveria estar no lugar de
(90º - β) para ser a "Lei de Snell".
Considerarei esta correção feita.

Seja xp = x ; yp = a; xp + xq = d; yq = b.

sen(α) = x/[(x² + a²)^(1/2)] e
sen(β) = (d - x)/[(d - x)² + b²]^(1/2).

t(pq) = t(pm) + t(mq) =>
=> t(pq) = [[V(x² + a²)]/u] + [[V((d - x)² + b²)]/v].

Como t(pq) é função de 'x', o mínimo pode ser encontrado por dt(pq)/dx = 0.

dt(pq)/dx = [(2.x)/(u.V(x² + a²))] +
+ (2.(d - x)².(-1))/(v.V(d - x)² + b²) = 0 <=>
<=> x/[u.V(x² + a²)] = (d - x)/[v.V((d - x)² + b²)] =>
=> sen(α)/u = sen(β)/v.

JOAO [ITA] escreveu:O ângulo β da sua figura deveria estar no lugar de
(90º - β) para ser a "Lei de Snell".
Considerarei esta correção feita.

Isso mesmo João. Acabei desenhando a figura errada. Que vacilo...

Ah,só mais uma coisa, voce poderia me explicar essa parte:

t(pq) = [[V(x² + a²)]/u] + [[V((d - x)² + b²)]/v].

Valeu!!

t(pm) = PM/u ;  t(mq) = MQ/v.

Ah, sim. Saquei. Achei que esse V em V(x² + a²) estava denotando alguma coisa, mas era V de raiz quadrada. Que vacilo...

Valeu JOAO [ITA]!!!