[Resolvido]Geometria Espacial - Tronco de Cone

por ALDRIN Sáb 17 Jul 2010, 14:40

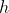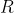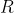Demonstrar que o volume de um tronco de cone reto de base circular em função da altura $h$ (do tronco) e dos raios das bases $R$ e $R$ , é dado por:

$V=\frac{1}{3}.\pi.\frac{h}{R-r}.(R^3-r^3)}$ .

por **Elcioschin** Ter 20 Jul 2010, 19:22

Seja h' a altura do conezinho que foi retirado do cone original:

h'/r = (h' + h)/R ----> Rh' = rh' + hr -----> h' = hr/(R - r) ----> Equação I

Volume do cone original ----> V = (1/3)*pi*R²*(h + h') -----> V = (1/3)*pi*R²*[h + hr/(R - r)] ----> V = (1/3)*pi*R³*h/(R - r)

Volume do conezinho -----> v = (1/3)*pi*r²*h' ----> v = 1/3)*pi*r²*(hr/(R - r) ----> v = (1/3)*pi*r³*h/(R - r)

Voume do tronco ----> Vt = V - v ----> Vt = (1/3)*pi*(R³ - r³)/(R - r)

Obs.: esta fórmula pode ainda ser reduzida dividindo (R³ - r³) por (R - r) -----> Vt = (1/3)*pi*(R² + Rr + r²)

por ALDRIN Sáb 24 Jul 2010, 11:43

Valeu Mestre.

por Conteúdo patrocinado

[Resolvido]Geometria Espacial - Tronco de Cone

[Resolvido]Geometria Espacial - Tronco de Cone

Re: [Resolvido]Geometria Espacial - Tronco de Cone

Re: [Resolvido]Geometria Espacial - Tronco de Cone

Re: [Resolvido]Geometria Espacial - Tronco de Cone

Um fórum livre e democrático.