Cone- Geometria Espacial

Um ralador de queijo tem a forma de cone circular reto de raio da base 4 cm e altura 10 cm. O queijo é ralado na base do cone e fica acumulado em seu interior (figura 1). Deseja-se retirar uma fatia de um queijo com a forma de cilindro circular reto de raio da base 8 cm e altura 6 cm, obtida por dois cortes perpendiculares à base, partindo do centro da base do queijo e formando um ângulo \alpha (figura 2), de forma que o volume de queijo dessa fatia corresponda a 90% do volume do ralador.



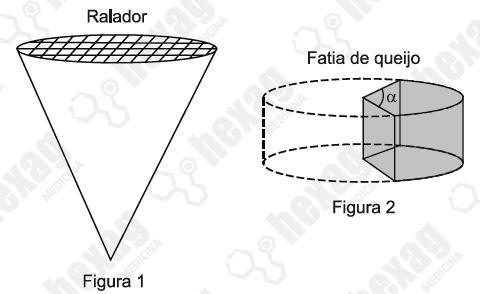
Nas condições do problema, \alpha  é igual a:
a) 45°.
b) 50°.
c) 55°.
d) 60°.
e) 65°.

Eu tentei fazer de uma forma que não deu certo...
Vcone= 160∏/3
Vqueijo=0,9Vcone ---> Vqueijo= 48∏

Olhando para a fatia de queijo, eu separei em um prisma triangular e meio cilindro.
Para o prisma: Área da base= (8*8*sen \alpha )/2
Vprisma=Ab*h ---> Vprisma= 192*sen \alpha

Para o meio cilindro: (2R)²= 8² + 8² -2*8*8*cos \alpha
R²= 32(1 - cos \alpha )
Vcilindro= 94∏ (1- cos \alpha )

Vqueijo= Vprisma + Vcilindro
48∏= 192*sen \alpha + 96∏( 1- cos \alpha )

Até tentei elevar os lados ao quadrado, mas não deu certo, e acho que não é esse o caminho, mas não sei o que fiz de errado...

Alguém  pode me ajudar??

Apenas regra de três:

\\V_{cone}=\frac{1}{3}\cdot \pi \cdot 16\cdot 10=\frac{160\pi }{3}\;cm^{3}\\\\V_{fatia}=\frac{9}{10}\cdot V_{cone}\rightarrow V_{fatia}=48\pi \;cm^{3}\\\\V_{queijo}=\pi \cdot 64\cdot 6=384\pi \;cm^{3}\\\\\frac{384\pi }{360^{\circ} }=\frac{48\pi }{\alpha }\rightarrow \alpha =45^{\circ}