Dúvida - teorema fundamental do cálculo

O Teorema Fundamental do Cálculo (parte 1) estabelece que se uma função g representa a integral definida de uma função f de a para b, sendo f contínua em [a,b], então g é necessariamente uma antiderivada de f. (e a parte 2 decorre disso, sabendo que qualquer antiderivada difere desta em particular por apenas uma constante)

Bem, minha dúvida é a seguinte: essa função g sempre existe? 

Isto é, posso sempre encontrar uma função que, para cada valor do domínio, o elemento correspondente na imagem fornece a área líquida sob a curva de f? (supondo f contínua no intervalo considerado). Isso é passível de argumentação/demonstração ou é mais intuitivo? 


Obrigado desde já!

Não é sempre que pode encontrar a primitiva.

Por exemplo a função seno integral :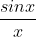   não tem primitiva em termos de funções elementares , e nem a função de gauss :  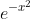 . Assim tbm ocorre com a função eliptica :  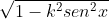 , com k diferente de 0 e 1, esta última é interessante , pois vários matemáticos estudaram esse tipo de função que ocorre quando tentamos calcular o comprimento de uma elipse e constataram que não existe primitiva, assim sendo nesses casos vc pode usar uma expansão em série e aproximar o quanto desejar.