Subespaço Vetorial
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Subespaço Vetorial
Subespaço Vetorial
Considere o subespaço de R^4 S = {(1,1,-2,4),(1,1,-1,2),(1,4,-4,8 )}. O vetor (2/3,1,-1,2) pertence a S ?
R: Pertence.
-------------------------------
To meia enrolada nessa matéria... já li um monte de vezes, mas não consigo entender muito bem ainda os conceitos...
To com essas dúvidas:
1) Esse vetor pertence ao subespaço porque depois de fazer a combinação linear vc vê que eles são LD ?
2) Se ele fosse LI, não pertenceria ao subespaço pq não existiria nenhuma ligação entre os vetores, certo ?
3) A combinação Linear, serve para nesses casos poder saber se os vetores são LD ou LI ?
Obrigada quem puder me ajudar.
Obs: Quanto tempo não acessava o fórum! Tava com saudades já
R: Pertence.
-------------------------------
To meia enrolada nessa matéria... já li um monte de vezes, mas não consigo entender muito bem ainda os conceitos...
To com essas dúvidas:
1) Esse vetor pertence ao subespaço porque depois de fazer a combinação linear vc vê que eles são LD ?
2) Se ele fosse LI, não pertenceria ao subespaço pq não existiria nenhuma ligação entre os vetores, certo ?
3) A combinação Linear, serve para nesses casos poder saber se os vetores são LD ou LI ?
Obrigada quem puder me ajudar.
Obs: Quanto tempo não acessava o fórum! Tava com saudades já

Cam™- Recebeu o sabre de luz

- Mensagens : 139
Data de inscrição : 22/07/2009
Localização : RJ
 Re: Subespaço Vetorial
Re: Subespaço Vetorial
Escrevendo o vetor (2/3,1,-1,2) como Combinação Linear dos vetores que compõe o Subespaço Vetorial do IR4 para verificar se ele pertence ao subespaço em questão ao não. Em caso afirmativo dizemos que ele é LD (linearmente dependente), e em caso negativo dizemos que ele é LI (linearmente independente).
a(1,1,-2,4) + b(1,1,-1,2) + c(1,4,-4,8 ) = (2/3,1,-1,2)
Assim:
&%20\\%20a%20+%20b%20+%204c%20=%201%20\hspace{10}%20(II)&%20\\%20-2a%20-%20b%20-4c%20=%20-1%20\hspace{10}%20(III)&%20\\%204a%20+%202b%20+%208c%20=%202%20\hspace{10}%20(IV)&%20\end{matrix}\right.)
Na Equação (I):
a + b = 2/3 - c
Substituindo na Equação (II):
(a + b) + 4c = 1
2/3 - c + 4c = 1
3c = 1 - 2/3
c = 1/9
Substituindo "c" em (I):
a + b = 2/3 - 1/9
a + b = 5/9 (V)
Substituindo "c" em (III):
-2a - b -4(1/9) = -1
-2a - b = -1 + 4/9
-2a -b = -5/9 (VI)
Utilizando o Método da Adição entre as Equações (V) e (VI):
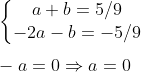
Substituindo "a" em (V):
0 + b = 5/9
b = 5/9
Portanto, pertence ao Subespaço Vetorial em questão!
a(1,1,-2,4) + b(1,1,-1,2) + c(1,4,-4,8 ) = (2/3,1,-1,2)
Assim:
Na Equação (I):
a + b = 2/3 - c
Substituindo na Equação (II):
(a + b) + 4c = 1
2/3 - c + 4c = 1
3c = 1 - 2/3
c = 1/9
Substituindo "c" em (I):
a + b = 2/3 - 1/9
a + b = 5/9 (V)
Substituindo "c" em (III):
-2a - b -4(1/9) = -1
-2a - b = -1 + 4/9
-2a -b = -5/9 (VI)
Utilizando o Método da Adição entre as Equações (V) e (VI):
Substituindo "a" em (V):
0 + b = 5/9
b = 5/9
Portanto, pertence ao Subespaço Vetorial em questão!
____________________________________________
"Há três coisas na vida que não voltam: As palavras, o tempo e as oportunidades."
Autor Desconhecido

aryleudo- Grande Mestre

- Mensagens : 2292
Data de inscrição : 01/10/2009
Idade : 41
Localização : Cascavel/CE - Brasil
 Re: Subespaço Vetorial
Re: Subespaço Vetorial
Muito obrigada aryleudo, entendi tudo!
Desculpe a demora em responder.
Desculpe a demora em responder.

Cam™- Recebeu o sabre de luz

- Mensagens : 139
Data de inscrição : 22/07/2009
Localização : RJ
 Re: Subespaço Vetorial
Re: Subespaço Vetorial
solução fantastica
YagoBB- Recebeu o sabre de luz

- Mensagens : 112
Data de inscrição : 31/12/2013
Idade : 28
Localização : rio de janeiro
 Tópicos semelhantes
Tópicos semelhantes» Verificação subespaço vetorial do espaço vetorial V
» Subespaço vetorial
» subespaço vetorial do R³
» Subespaço Vetorial
» Subespaço vetorial
» Subespaço vetorial
» subespaço vetorial do R³
» Subespaço Vetorial
» Subespaço vetorial
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












