Função Logarítmica

por adrianybrito Qui 24 Abr 2014, 22:53

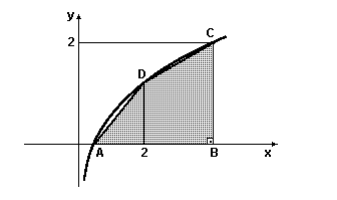
(UFJF) Na figura a seguir, encontram-se representados o gráfico da função f: (0,∞), definida por, f(x) log x (com base 2)
e o polígono ABCD. Os pontos A, C e D estão sobre o gráfico de f.
Os pontos A e B estão sobre o eixo das abscissas. O ponto C tem ordenada 2, o ponto D
tem abscissa 2 e BC é perpendicular ao eixo das abscissas.
Sabendo que os eixos estão graduados em centímetros, a área do polígono ABCD é:
a) 2,5 cm2
.
b) 3 cm2
.
c) 3,5 cm2
.
d) 4 cm2
.
e) 4,5 cm2
R:c
Função Logarítmica 2nkq32h

por PedroCunha Qui 24 Abr 2014, 23:13

Olá.

Vamos descobrir a ordenada de D:

y = log_2 x .:. y_d = log_2 2 .:. y_d = 1

Agora, vamos descobrir a abcissa de c, que é igual a abcissa de B:

2 = log_2 x_b .:. x_b = 4

Então: D(2,1) ; B(4,0) ; C(4,2)

Note que A é (x_a,0). Vamos encontrar x_a:

0 = log_2 x_a .:. x_a = 1 --> A(1,0)

A área de ABCD é igual a área do triângulo ADx_d + a área do trapézio Dx_dCB. Então:

S = (2-1)*1/2 + (1 + 2) * 2/2 .:. S = 1/2 + 3 .:. S = 3,5 cm²

Att.,
Pedro

Função Logarítmica

Função Logarítmica

Re: Função Logarítmica

Um fórum livre e democrático.