Produtos Notáveis/ Fatoração
3 participantes
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
 Produtos Notáveis/ Fatoração
Produtos Notáveis/ Fatoração
Se a+b+c=0. Calcule o equivalente à:
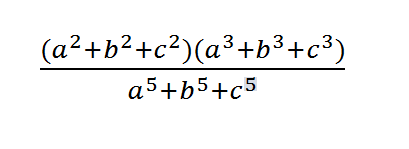
https://i.gyazo.com/6a98b421f83a3433d93e8f551e7d41ea.png
A resposta é 6/5
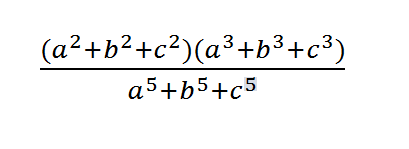
https://i.gyazo.com/6a98b421f83a3433d93e8f551e7d41ea.png
A resposta é 6/5
L.Lawliet- Mestre Jedi

- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
 Re: Produtos Notáveis/ Fatoração
Re: Produtos Notáveis/ Fatoração
Veja a questão abaixo e use a mesma ideia:
https://pir2.forumeiros.com/t64160-fracoes-obm
https://pir2.forumeiros.com/t64160-fracoes-obm

Luck- Grupo
Velhos amigos do Fórum
- Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 32
Localização : RJ
 Re: Produtos Notáveis/ Fatoração
Re: Produtos Notáveis/ Fatoração
Fiz por polinômios, deu uma simplificada enorme 
Tome um polinômio P(x)= x³-kx²+px-q onde a, b e c são raízes.
Por girard, a soma das raízes tem de ser k, mas a+b+c=0, logo k=0.
Nosso polinômio fica assim :
P(x)= x³+px-q
I) Perceba que :
a³+pa-q = 0
b³+pb-q = 0
c³+pc-q = 0
Se somarmos, temos que:
(a³+b³+c³)+p(a+b+c)-3q=0
(a³+b³+c³)+p(0)-3q=0
(a³+b³+c³)=3q
II) Se multiplicarmos por a², b² e c², simultaneamente, em cada termo, temos:
a^5+pa^3-qa^2 = 0
b^5+pb^3-qb^2 = 0
c^5+pc^3-qc^2 = 0
Somando todos, temos :
(a^5+b^5+c^5)+p(a^3+b^3+c^3)-q(a^2+b^2+c^2) = 0
a^3+b^3+c^3 já temos:
(a^5+b^5+c^5)+3qp-q(a^2+b^2+c^2) = 0
Mas o que seria a^2+b^2+c^2 ? Por produto notável, temos:
(a+b+c)^2=a^2+b^2+c^2+2(ab+ac+bc)
(a+b+c)^2=0^2=0=a^2+b^2+c^2+2(ab+ac+bc)
Portanto, a^2+b^2+c^2=-2(ab+ac+bc):
Mas por girrard, a relação (ab+ac+bc) = p (Claro, no polinômio P(x)=x³+px-q) :
a^2+b^2+c^2=-2p
III) Substituindo em (a^5+b^5+c^5)+3qp-q(a^2+b^2+c^2) = 0 :
(a^5+b^5+c^5)+3qp-q(-2p)= 0
(a^5+b^5+c^5)=-(3qp-q(-2p)) = -5qp
IV) Finalmente, temos que :
(a^2+b^2+c^2).(a^3+b^3+c^3)/(a^5+b^5+c^5) = (-2p).(3q)/(-5pq)
= 6/5
Tome um polinômio P(x)= x³-kx²+px-q onde a, b e c são raízes.
Por girard, a soma das raízes tem de ser k, mas a+b+c=0, logo k=0.
Nosso polinômio fica assim :
P(x)= x³+px-q
I) Perceba que :
a³+pa-q = 0
b³+pb-q = 0
c³+pc-q = 0
Se somarmos, temos que:
(a³+b³+c³)+p(a+b+c)-3q=0
(a³+b³+c³)+p(0)-3q=0
(a³+b³+c³)=3q
II) Se multiplicarmos por a², b² e c², simultaneamente, em cada termo, temos:
a^5+pa^3-qa^2 = 0
b^5+pb^3-qb^2 = 0
c^5+pc^3-qc^2 = 0
Somando todos, temos :
(a^5+b^5+c^5)+p(a^3+b^3+c^3)-q(a^2+b^2+c^2) = 0
a^3+b^3+c^3 já temos:
(a^5+b^5+c^5)+3qp-q(a^2+b^2+c^2) = 0
Mas o que seria a^2+b^2+c^2 ? Por produto notável, temos:
(a+b+c)^2=a^2+b^2+c^2+2(ab+ac+bc)
(a+b+c)^2=0^2=0=a^2+b^2+c^2+2(ab+ac+bc)
Portanto, a^2+b^2+c^2=-2(ab+ac+bc):
Mas por girrard, a relação (ab+ac+bc) = p (Claro, no polinômio P(x)=x³+px-q) :
a^2+b^2+c^2=-2p
III) Substituindo em (a^5+b^5+c^5)+3qp-q(a^2+b^2+c^2) = 0 :
(a^5+b^5+c^5)+3qp-q(-2p)= 0
(a^5+b^5+c^5)=-(3qp-q(-2p)) = -5qp
IV) Finalmente, temos que :
(a^2+b^2+c^2).(a^3+b^3+c^3)/(a^5+b^5+c^5) = (-2p).(3q)/(-5pq)
= 6/5

VictorCoe- Fera

- Mensagens : 530
Data de inscrição : 20/02/2012
Idade : 27
Localização : Fortaleza/Ceará
 Re: Produtos Notáveis/ Fatoração
Re: Produtos Notáveis/ Fatoração
Nossa Luck, foi da mesma forma que eu fiz, por somas de newton. Deu um trabalhão fazê-la 

VictorCoe- Fera

- Mensagens : 530
Data de inscrição : 20/02/2012
Idade : 27
Localização : Fortaleza/Ceará
 Re: Produtos Notáveis/ Fatoração
Re: Produtos Notáveis/ Fatoração
galera, conseguir desenvolver por fatoração. Mas valeu luck e VictorCoe!!!
L.Lawliet- Mestre Jedi

- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
 Tópicos semelhantes
Tópicos semelhantes» Fatoração e Produtos Notáveis
» Produtos Notáveis/ Fatoração
» Produtos Notáveis e Fatoração IV
» Produtos Notáveis e fatoração
» Produtos Notáveis e fatoração
» Produtos Notáveis/ Fatoração
» Produtos Notáveis e Fatoração IV
» Produtos Notáveis e fatoração
» Produtos Notáveis e fatoração
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












