Semelhança de triangulos
4 participantes
Página 1 de 1
Semelhança de triangulos
por LaraCaroline Sex 18 Abr 2014, 20:16
Na figura a seguir, os triângulos ABC e AB’C’ são
semelhantes. Se AC = 4AC’, então o perímetro de AB’C’,
dividido pelo perímetro de ABC, é igual a
a) 1/8
b) 1/6
c) 1/4
d) 1/2
e) 1
a resposta é a C.
Gostaria que alguém me ajudasse detalhadamente, estou com um pouco de duvida em montar a semelhança.
semelhantes. Se AC = 4AC’, então o perímetro de AB’C’,
dividido pelo perímetro de ABC, é igual a
a) 1/8
b) 1/6
c) 1/4
d) 1/2
e) 1
a resposta é a C.
Gostaria que alguém me ajudasse detalhadamente, estou com um pouco de duvida em montar a semelhança.
LaraCaroline- Padawan
- Mensagens : 78
Data de inscrição : 03/03/2014
Idade : 27
Localização : Saquarema-RJ
Re: Semelhança de triangulos
por gustavolol2 Sex 18 Abr 2014, 21:07
Olá,
Se a razão de semelhança de dois triângulos é k, então o a razão entre os perímetros é k.
Se AC = 4AC’ , a razão de semelhança é k=1/4.
Razão entre os perímetros também será 1/4.
Se a razão de semelhança de dois triângulos é k, então o a razão entre os perímetros é k.
Se AC = 4AC’ , a razão de semelhança é k=1/4.
Razão entre os perímetros também será 1/4.
gustavolol2- Recebeu o sabre de luz
- Mensagens : 123
Data de inscrição : 17/06/2012
Idade : 28
Localização : Minas Gerais
LaraCaroline- Padawan
- Mensagens : 78
Data de inscrição : 03/03/2014
Idade : 27
Localização : Saquarema-RJ
Outra forma de resolução
por Patrick G. Nascimento Qua 17 maio 2017, 11:23
Não estou compreendendo essa resolução, alguém teria uma diferente?
Patrick G. Nascimento- Iniciante
- Mensagens : 21
Data de inscrição : 17/02/2017
Idade : 28
Localização : Ji-Paraná RO
Re: Semelhança de triangulos
por vitortaques Qua 17 maio 2017, 16:09
Patrick G. Nascimento,
Como o enunciado fala que são triângulo semelhantes entenda que seus ângulos são iguais e lados proporcionais. Com isso, conforme enunciado, temos que o triângulo ∆ABC tem o lado AC 4 vezes maior que o lado AC' do triângulo ∆AB'C'. Dessa forma, sabemos que ∆ABC é 4 vezes maior que triângulo ∆AB'C'. Como a questão pede a razão entre o perímetro de ∆AB'C' e ∆ABC. Temos que:
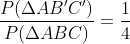
Espero ter ajudado. Abraços
Como o enunciado fala que são triângulo semelhantes entenda que seus ângulos são iguais e lados proporcionais. Com isso, conforme enunciado, temos que o triângulo ∆ABC tem o lado AC 4 vezes maior que o lado AC' do triângulo ∆AB'C'. Dessa forma, sabemos que ∆ABC é 4 vezes maior que triângulo ∆AB'C'. Como a questão pede a razão entre o perímetro de ∆AB'C' e ∆ABC. Temos que:
Espero ter ajudado. Abraços
vitortaques- Iniciante
- Mensagens : 39
Data de inscrição : 20/02/2016
Idade : 28
Localização : Ji-Paraná - RO
Re: Semelhança de triangulos
por Patrick G. Nascimento Qua 17 maio 2017, 16:47
Entendi claramente!!! Valeu pela força Vitortaques, Abraço.
Patrick G. Nascimento- Iniciante
- Mensagens : 21
Data de inscrição : 17/02/2017
Idade : 28
Localização : Ji-Paraná RO
Tópicos semelhantes» Semelhança de triângulos
» Semelhança de Triângulos
» Semelhança de Triângulos
» Semelhança de triangulos
» Semelhança de triângulos
» Semelhança de Triângulos
» Semelhança de Triângulos
» Semelhança de triangulos
» Semelhança de triângulos
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
