Geometria - Cilindros

Olá caros amigos; requisito a ajuda dos mestres no tocante à resolução desta questão, a qual não consigo resolver de maneira alguma.
Obrigado desde já e desculpem a ignorância. Abraços

A empresa SWED celulose faz o transporte de seus rolos em containeres num formato de um cilindro. Em cada um deles são transportados três rolos de celulose de raio iguala 1 m, tangentes entre si dois a dois e os três tangentes ao cilindro que os contém. Contudo, a empresa está interessada em descobrir o espaço que fica vago entre os rolos de celulose e o container que os contém, para preenchê-lo com resíduos de papel. Para conhecer o espaço vago, é necessário determinar o raio do cilindro que contém os três cilindros pequenos. Esse raio é igual:

A) m. 
B) +1 m. 
C)  .
D)  + 2 m. 
E) m.

R: E

ninosninos escreveu:Olá caros amigos; requisito a ajuda dos mestres no tocante à resolução desta questão, a qual não consigo resolver de maneira alguma.
Obrigado desde já e desculpem a ignorância. Abraços

A empresa SWED celulose faz o transporte de seus rolos em containeres num formato de um cilindro. Em cada um deles são transportados três rolos de celulose de raio iguala 1 m, tangentes entre si dois a dois e os três tangentes ao cilindro que os contém. Contudo, a empresa está interessada em descobrir o espaço que fica vago entre os rolos de celulose e o container que os contém, para preenchê-lo com resíduos de papel. Para conhecer o espaço vago, é necessário determinar o raio do cilindro que contém os três cilindros pequenos. Esse raio é igual:

A) m. 
B) +1 m. 
C)  .
D)  + 2 m. 
E) m.

R: E

Boa noite,

Faça um esboço de um círculo e dentro dele, tangentes entre si e ao círculo, três círculos de igual diâmetro (mesmo raio).
Agora marque com os pontos O1, O2 e O3 os centros desses três círculos.
A seguir, liga-os entre si, formando, assim, um triângulo equilátero.

Prosseguindo, trace as três alturas desse triângulo equilátero, identificando com a letra O4 o cruzamento das três alturas;identifique os pés das alturas com as letras M, N, P.

Esse ponto, O4, será o centro do círculo maior, aquele que contém os 3 círculos menores.

Note que cada lado do triângulo equilátero mede 2 m, ou seja, 1 m + 1 m, distância entre cada 2 centros O1-O2, O1-O3, O2-O3.

Ligue o centro O4 com O1 (acima dele) e prolongue de uma medida igual a MO1, identificando seu extremo livre com a letra C.
A medida do segmento de reta CO4 é igual ao Raio do círculo maior.

Agora, vamos aos cálculos:
Cada lado do triângulo equilátero, como já foi dito, mede 2 raios.
Cada raio medindo 1 m, perfaz, então 2*1 m = 2 metros.

Medida de cada altura:
Lado * √3/2 = 2 m * √3/2 = √3 m

Essa é, então, a medida de cada altura, ou de cada mediana, traçada nesse triângulo equilátero.
Como as medianas cruzam-se a 2/3 de seus respectivos vértices, temos que a medida desde O4 até O1 é igual a:
2/3 * √3 m = 2√3/3 m.

Portanto, a medida procurada do Raio do círculo maior é:
2√3/3 m + r = 2√3/3 m + 1 m = (2√3/3 + 3/3) m = (2√3 + 3)/3 m 

Alternativa (E)




Um abraço.

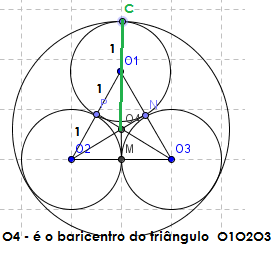
Ilustrando a resolução do amigo Ivomilton.

Agradeço imensamente a ajuda. Desejo-lhes uma boa semana e grandes abraços.