Área hachurada

por Otavinhoo Qui 26 Set 2013, 13:41

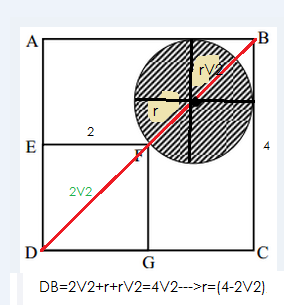
Na figura abaixo, ABCD é um quadrado com 4cm de lado e DEFG é um quadrado com 2cm de lado. Nela desenhamos uma circunferência que passa por F e é tangente aos lados AB e BC do quadrado grande. A área hachurada, limitada por esta circunferência, é:

Área hachurada 5n19

R: 8Pi(3 - 2√2) cm²
R

por Luck Qui 26 Set 2013, 15:11

Seja O o centro da circunfererência,trace o raio partindo de F a O , e o raio tangenciando os dois lados à O, sendo DG = 2 , GC = 2 , note que a projeção horizontal de FO vale 2-R e a vertical também 2-R, então temos um triângulo retângulo isósceles com hipotenusa R, catetos 2-R . sen45º = (2-R)/R ∴ √2/2 = (2-R)/R ∴ R = 2(2-√2)
S = piR²
S = pi[2(2-√2)]²
S = 8pi(3-2√2) cm²
obs. se nao conseguir ver fala, que faça um desenho..

por **raimundo pereira** Qui 26 Set 2013, 15:33

por Otavinhoo Qui 26 Set 2013, 19:44

Luck pode fazer o desenho? Não entendi muito bem o do Raimundo. ://

por **raimundo pereira** Qui 26 Set 2013, 20:14

Olá Otavinho ,
Você concorda que a área pedida é igual a área do círculo de raio r. Então vamos achar esse raio.

É sabido que a diagonal de um quadrado de lado L mede LV2. OK

Veja que o quadrado que envolve o círculo, nós não sabemos o seu raio, por isso o chamamos de r.

Você concorda que a diagonal do quadrado maior é 4.V2 . Ok ---->(1)
Mas, a que é igual essa diagonal?
É igual a diagonal do quadrado menor de lado 2,que é ( 2V2 )+ r + r V2 ---->(2)

Igualando 1 e 2 vc acha o valor de r.-->r=4-2V2

A área pedida é S=pir²-->pi(4-2V2)²=8(3-2V2)cm²

att