DIVISÃO

por georges123 Dom Set 08 2013, 14:06

Ache todos os inteiros estritamente positivos com a seguinte propriedade: tenham resto 6 quando divididos por 11 e resto 3 quando divididos por 7.

( essa não tem gabarito )

Agradeço a quem tentar me ajudar.

por Man Utd Dom Set 08 2013, 16:13

utilizando o teorema do resto chinês:

$DIVISÃO Gif$

substituindo (I) na primeira congruência temos:

$DIVISÃO Gif$

substituindo (II) em (I) temos:

$DIVISÃO Gif$

com c pertencente aos inteiros.

att mais, Very Happy

por georges123 Seg Set 09 2013, 11:43

OLÁ
Bom Dia
$DIVISÃO Gif$

ESSA PARTE EU NÃO ENTENDI, TERIA COMO EXPLICÁ-LA NOVAMENTE ?

por Man Utd Seg Set 09 2013, 20:46

sim.posso explicar.

primeiro perceba que eu substituir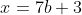 $DIVISÃO Gif$ em $DIVISÃO Gif$ , então:

$DIVISÃO Gif$

agora vou subtraí 3 dos dois lados ficamos com:

$DIVISÃO Gif$

perceba que nosso objetivo é obter o "b" isolado para isso , então vamos multiplicar por -3 os dois lados já que:

$DIVISÃO Gif$

então ficaremos com:

$DIVISÃO Gif$

agora só apliquei a definição de congruência módulo, aquela que diz a≡ b mod(m), se e somente se a-b=k*m,onde k pertence aos inteiros.ficando com:

$DIVISÃO Gif$

qualquer dúvida,estamos a disposição. Very Happy